2025年有一套初中各地市期末真题八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年有一套初中各地市期末真题八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
19. 阅读下面材料:
直尺、圆规、三角板等是常用的数学工具,利用这些工具作图或者画图,并理解其中的数学原理,是数学学习中探究及解决问题的主要方式之一.下面分别给出了得到已知角的平分线的两种方法.

完成下面问题:
(1)请证明方法一中的$OC$是$\angle AOB$的平分线;
(2)直接写出方法二中的$OC$是$\angle AOB$的平分线的依据.
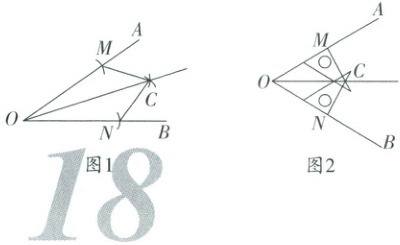
直尺、圆规、三角板等是常用的数学工具,利用这些工具作图或者画图,并理解其中的数学原理,是数学学习中探究及解决问题的主要方式之一.下面分别给出了得到已知角的平分线的两种方法.

完成下面问题:
(1)请证明方法一中的$OC$是$\angle AOB$的平分线;
(2)直接写出方法二中的$OC$是$\angle AOB$的平分线的依据.

答案:
19.
(1)证明:由作图方法,得$OM = ON$,$MC = NC$.
在$\triangle OMC$和$\triangle ONC$中,$\begin{cases}OM = ON,\\OC = OC,\\MC = NC.\end{cases}$
$\therefore\triangle OMC\cong\triangle ONC(SSS)$,$\therefore\angle AOC = \angle BOC$,
即$OC$为$\angle AOB$的平分线.
(2)解:角的内部到角的两边的距离相等的点在角的平分线上.
(1)证明:由作图方法,得$OM = ON$,$MC = NC$.
在$\triangle OMC$和$\triangle ONC$中,$\begin{cases}OM = ON,\\OC = OC,\\MC = NC.\end{cases}$
$\therefore\triangle OMC\cong\triangle ONC(SSS)$,$\therefore\angle AOC = \angle BOC$,
即$OC$为$\angle AOB$的平分线.
(2)解:角的内部到角的两边的距离相等的点在角的平分线上.
查看更多完整答案,请扫码查看


