《2025年有一套初中各地市期末真题八年级数学上册人教版》

23. (13 分)【问题呈现】
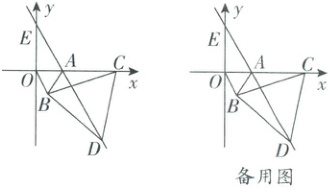
如图,在平面直角坐标系中,点 $ A $ 的坐标为 $ (1,0) $,以线段 $ OA $ 为边在第四象限内作等边三角形 $ AOB $,点 $ C $ 为 $ x $ 轴正半轴上一动点 $ (OC ＞ 1) $,连接 $ BC $,以线段 $ BC $ 为边在第四象限内作等边三角形 $ CBD $,连接 $ DA $ 并延长,交 $ y $ 轴于点 $ E $.
【问题提出】
(1) 在此过程中,线段 $ OC $ 与 $ AD $ 有何数量关系? 并证明你的结论;
【尝试探究】
(2) 在点 $ C $ 的运动过程中, $ \angle CAD $ 的度数是否会发生变化? 如果不变,请求出 $ \angle CAD $ 的度数,如果改变,请说明理由;
【拓展延伸】
(3) 当点 $ C $ 运动到什么位置时,以 $ A,E,C $ 为顶点的三角形是等腰三角形?

答案： 23.解：
(1)$OC = AD$。证明如下：
∵△AOB，△CBD都是等边三角形，
∴$OB = AB$，$CB = DB$，$∠ABO = ∠DBC = 60°$，
∴$∠ABO + ∠ABC = ∠DBC + ∠ABC$，即$∠OBC = ∠ABD$，
∴△OBC≌△ABD(SAS)，
∴$OC = AD$。
(2)点C在运动过程中，∠CAD的度数不会发生变化。
∵△AOB是等边三角形，
∴$∠BOA = ∠OAB = 60°$。
∵△OBC≌△ABD，
∴$∠BAD = ∠BOC = 60°$，
∴$∠CAD = 180° - ∠OAB - ∠BAD = 180° - 60° - 60° = 60°$，
∴点C在运动过程中，∠CAD的度数不变，∠CAD = 60°。
(3)
∵△OBC≌△ABD，
∴$∠BOC = ∠BAD = 60°$。
又
∵$∠OAB = 60°$，
∴$∠OAE = 180° - 60° - 60° = 60°$，
∴$∠EAC = 120°$，$∠OEA = 30°$，
∴以A，E，C为顶点的三角形是等腰三角形时，AE和AC是腰。
在Rt△AOE中，$OA = 1$，$∠OEA = 30°$，
∴$AE = 2$，
∴$AC = AE = 2$，
∴$OC = OA + AC = 1 + 2 = 3$，
∴当点C的坐标为(3,0)时，以A，E，C为顶点的三角形是等腰三角形。