2025年有一套初中各地市期末真题八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年有一套初中各地市期末真题八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 如图所示为钢架的示意图,$ \angle A = 25^{\circ} $,焊上等长的钢条 $ P_1P_2 $,$ P_2P_3 $,…来加固钢架. 若 $ P_1A = P_1P_2 $,则这样的钢条至多需要(
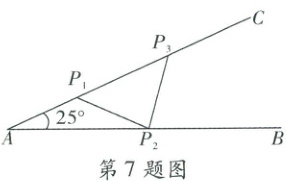
A.$ 2 $ 根
B.$ 3 $ 根
C.$ 4 $ 根
D.$ 5 $ 根
B
)
A.$ 2 $ 根
B.$ 3 $ 根
C.$ 4 $ 根
D.$ 5 $ 根
答案:
7.B [解析]
∵$P_1A = P_1P_2$,
∴$\angle A = \angle P_1P_2A = 25^{\circ}$,
∴$\angle P_2P_1P_3 = \angle A + \angle P_1P_2A = 50^{\circ}$.
若$P_2P_3$可以焊接,
∵$P_1P_2 = P_2P_3$,
∴$\angle P_1P_3P_2 = \angle P_2P_1P_3 = 50^{\circ}$,
∴$\angle P_1P_2P_3 = 80^{\circ}$.
若$P_3P_4$可以焊接,则$\angle P_3P_2P_4 = 75^{\circ}$.
∵$P_2P_3 = P_3P_4$,
∴$\angle P_3P_4P_2 = 75^{\circ}$.
若$P_4P_5$可以焊接,则$\angle P_5P_3P_4 = 100^{\circ}$.
∵$P_3P_4 = P_4P_5$,
∴$\angle P_4P_5P_3 = 100^{\circ}$,
∴此时不能继续焊接.
综上所述,这样的钢条至多需要3根.故选:B.
∵$P_1A = P_1P_2$,
∴$\angle A = \angle P_1P_2A = 25^{\circ}$,
∴$\angle P_2P_1P_3 = \angle A + \angle P_1P_2A = 50^{\circ}$.
若$P_2P_3$可以焊接,
∵$P_1P_2 = P_2P_3$,
∴$\angle P_1P_3P_2 = \angle P_2P_1P_3 = 50^{\circ}$,
∴$\angle P_1P_2P_3 = 80^{\circ}$.
若$P_3P_4$可以焊接,则$\angle P_3P_2P_4 = 75^{\circ}$.
∵$P_2P_3 = P_3P_4$,
∴$\angle P_3P_4P_2 = 75^{\circ}$.
若$P_4P_5$可以焊接,则$\angle P_5P_3P_4 = 100^{\circ}$.
∵$P_3P_4 = P_4P_5$,
∴$\angle P_4P_5P_3 = 100^{\circ}$,
∴此时不能继续焊接.
综上所述,这样的钢条至多需要3根.故选:B.
8. 如图,已知 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle A = 30^{\circ} $,$ BD $ 平分 $ \angle CBA $,且交 $ AC $ 于点 $ D $,$ AC = 1 $,那么 $ AD $ 的长是
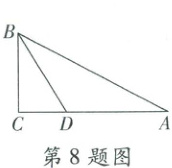
$\frac{2}{3}$
.
答案:
8.$\frac{2}{3}$
9. 如图,一艘轮船由海平面上 $ C $ 地出发向南偏西 $ 25^{\circ} $ 方向行驶 $ 50 $ 海里到达 $ B $ 地,再由 $ B $ 地向北偏西 $ 35^{\circ} $ 方向行驶 $ 50 $ 海里到达 $ A $ 地,则 $ A $,$ C $ 两地相距
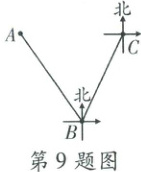
50
海里.
答案:
9.50
10. 如图,已知 $ AB = BC = AD $,$ AD \perp BC $ 于点 $ E $,$ AC \perp CD $,若 $ CD = \frac{3}{5} $,则 $ \triangle ACD $ 的面积为
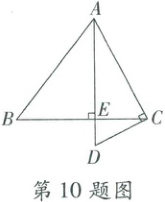
$\frac{9}{25}$
.
答案:
10.$\frac{9}{25}$
11. 如图,$ \triangle ABC $,$ \triangle CDE $ 都是等边三角形,将 $ \triangle CDE $ 绕点 $ C $ 旋转,使得点 $ A $,$ D $,$ E $ 在同一直线上,连接 $ BE $. 若 $ BE = 1 $,$ AE = 4 $,则 $ CE $ 的长是
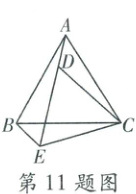
3
.
答案:
11.3
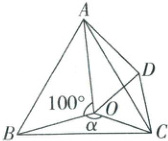
12. 如图,$ O $ 是等边三角形 $ ABC $ 内一点,$ \angle AOB = 100^{\circ} $,$ \angle BOC = \alpha $. 以 $ OC $ 为一边作等边三角形 $ OCD $,连接 $ AC $,$ AD $.
(1)当 $ \alpha = 150^{\circ} $ 时,试判断 $ \triangle AOD $ 的形状,并说明理由;
(2)当 $ \triangle AOD $ 是等腰三角形时,求 $ \alpha $ 的度数.
(1)当 $ \alpha = 150^{\circ} $ 时,试判断 $ \triangle AOD $ 的形状,并说明理由;
(2)当 $ \triangle AOD $ 是等腰三角形时,求 $ \alpha $ 的度数.

答案:
12.解:
(1)△AOD是直角三角形.理由如下:
∵△ABC,△OCD是等边三角形,
∴$BC = AC$,$OC = DC$,$\angle ACB = \angle OCD = 60^{\circ}$,
∴$\angle BCO = \angle ACD$.
在$\triangle BOC$和$\triangle ADC$中,$\begin{cases}OC = DC,\\\angle BCO = \angle ACD,\\BC = AC,\end{cases}$
∴$\triangle BOC \cong \triangle ADC(SAS)$,
∴$\angle BOC = \angle ADC$.
∵$\angle BOC = \alpha = 150^{\circ}$,$\angle ODC = 60^{\circ}$,
∴$\angle ADO = 150^{\circ} - 60^{\circ} = 90^{\circ}$,
∴$\triangle ADO$是直角三角形.
(2)同
(1),得$\triangle BOC \cong \triangle ADC$,
∴$\angle BOC = \angle ADC = \alpha$,
∴$\angle AOD = 360^{\circ} - 100^{\circ} - 60^{\circ} - \alpha = 200^{\circ} - \alpha$,$\angle ADO = \alpha - 60^{\circ}$,
∴$\angle OAD = 180^{\circ} - \angle AOD - \angle ADO = 40^{\circ}$.
①要使$AO = AD$,需$\angle AOD = \angle ADO$,
∴$200^{\circ} - \alpha = \alpha - 60^{\circ}$,
∴$\alpha = 130^{\circ}$.
②要使$OA = OD$,需$\angle OAD = \angle ADO$,
∴$40^{\circ} = \alpha - 60^{\circ}$,
∴$\alpha = 100^{\circ}$.
③要使$OD = AD$,需$\angle OAD = \angle AOD$,
∴$40^{\circ} = 200^{\circ} - \alpha$,
∴$\alpha = 160^{\circ}$.
综上所述,当$\triangle AOD$是等腰三角形时,$\alpha$为$130^{\circ}$或$100^{\circ}$或$160^{\circ}$.
(1)△AOD是直角三角形.理由如下:
∵△ABC,△OCD是等边三角形,
∴$BC = AC$,$OC = DC$,$\angle ACB = \angle OCD = 60^{\circ}$,
∴$\angle BCO = \angle ACD$.
在$\triangle BOC$和$\triangle ADC$中,$\begin{cases}OC = DC,\\\angle BCO = \angle ACD,\\BC = AC,\end{cases}$
∴$\triangle BOC \cong \triangle ADC(SAS)$,
∴$\angle BOC = \angle ADC$.
∵$\angle BOC = \alpha = 150^{\circ}$,$\angle ODC = 60^{\circ}$,
∴$\angle ADO = 150^{\circ} - 60^{\circ} = 90^{\circ}$,
∴$\triangle ADO$是直角三角形.
(2)同
(1),得$\triangle BOC \cong \triangle ADC$,
∴$\angle BOC = \angle ADC = \alpha$,
∴$\angle AOD = 360^{\circ} - 100^{\circ} - 60^{\circ} - \alpha = 200^{\circ} - \alpha$,$\angle ADO = \alpha - 60^{\circ}$,
∴$\angle OAD = 180^{\circ} - \angle AOD - \angle ADO = 40^{\circ}$.
①要使$AO = AD$,需$\angle AOD = \angle ADO$,
∴$200^{\circ} - \alpha = \alpha - 60^{\circ}$,
∴$\alpha = 130^{\circ}$.
②要使$OA = OD$,需$\angle OAD = \angle ADO$,
∴$40^{\circ} = \alpha - 60^{\circ}$,
∴$\alpha = 100^{\circ}$.
③要使$OD = AD$,需$\angle OAD = \angle AOD$,
∴$40^{\circ} = 200^{\circ} - \alpha$,
∴$\alpha = 160^{\circ}$.
综上所述,当$\triangle AOD$是等腰三角形时,$\alpha$为$130^{\circ}$或$100^{\circ}$或$160^{\circ}$.
查看更多完整答案,请扫码查看


