《2025年有一套初中各地市期末真题八年级数学上册人教版》

18. (本小题7分)学习过等边三角形，小丽用折纸的方法裁出一个等边三角形. 如图，先将正方形纸片对折后展开，折痕为$MN$. 点$E$在线段$BN$上，连接$AE$，将$AB$沿$AE$折叠，点$B$落在$MN$上的点$H$处，连接$AH,DH$，沿$AH$和$DH$裁剪得到$\triangle DHA$，则$\triangle DHA$即为等边三角形，请给予证明.

答案： 18.证明：
∵四边形ABCD是正方形，
∴AD = AB。
由折叠的性质，得AH = AB。
∵MN是正方形ABCD的对称轴，
∴MN垂直平分AD，
∴DH = AH，
∴DH = AH = AD，
∴△DHA是等边三角形。

19. (本小题8分)如图，在$\triangle ABC$中，$AB = AC$，$D,A,E$三点都在直线$m$上，并且有$\angle BDA=\angle AEC=\angle BAC=\alpha$. 若$DE = 10$，$BD = 3$，求$CE$的长.

答案： 19.解：
∵∠AEC = ∠BAC = α，
∴∠ECA + ∠CAE = 180° - α，∠BAD + ∠CAE = 180° - α，
∴∠ECA = ∠BAD。
在△BAD和△ACE中，$\begin{cases}∠BDA = ∠AEC,\\AB = AC,\end{cases}$
∴△BAD ≌ △ACE(AAS)，
∴CE = AD，AE = BD = 3。
∵DE = AD + AE = 10，
∴AD = DE - AE = 10 - 3 = 7，
∴CE = 7。

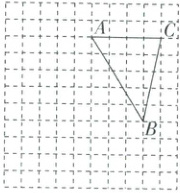
20. (本小题9分)格点三角形$ABC$的三个顶点的坐标分别为$A(0,3),B(3,-2),C(4,3)$.
(1) 请在图中画出适当的平面直角坐标系；
(2) 请画出$\triangle ABC$关于纵轴对称的$\triangle A_{1}B_{1}C_{1}$；
(3) 在横轴上找一点$P$，使$PA + PC$最短，并在图中标出点$P$的位置.

答案：
20.解：
(1)如图，平面直角坐标系即为所求。
(2)如图，△A₁B₁C₁即为所求。
(3)如图，取点A关于x轴的对称点A'，连接A'C，交x轴于点P，连接AP，
此时PA + PC = PA' + PC = A'C，为最小值，
则点P即为所求。