2025年有一套初中各地市期末真题八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年有一套初中各地市期末真题八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
13. 如图,$\triangle ABC$ 中,$\angle B < \angle C$,$AD \perp BC$ 于点 $D$,$AE$ 平分 $\angle BAC$ 交 $BC$ 于点 $E$。
(1)当 $\angle B = 30^{\circ}$,$\angle C = 50^{\circ}$ 时,求 $\angle DAE$ 的度数;
(2)猜想:$\angle DAE$ 与 $\angle B$,$\angle C$ 有什么关系,并说明理由。
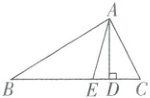
(1)当 $\angle B = 30^{\circ}$,$\angle C = 50^{\circ}$ 时,求 $\angle DAE$ 的度数;
(2)猜想:$\angle DAE$ 与 $\angle B$,$\angle C$ 有什么关系,并说明理由。

答案:
13.解:
(1)$\because \angle B = 30^{\circ}, \angle C = 50^{\circ}$,
$\therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 100^{\circ}$.
$\because AE$平分$\angle BAC$,
$\therefore \angle CAE = \frac{1}{2}\angle BAC = 50^{\circ}$.
$\because AD \perp BC, \angle C = 50^{\circ}$,
$\therefore \angle DAC = 90^{\circ} - 50^{\circ} = 40^{\circ}$,
$\therefore \angle DAE = \angle CAE - \angle CAD = 50^{\circ} - 40^{\circ} = 10^{\circ}$.
(2)$\angle DAE = \frac{1}{2}(\angle C - \angle B)$.理由如下:
$\because AD,AE$分别是$\triangle ABC$的高和角平分线,
答案
$\therefore \angle CAE = \frac{1}{2}\angle BAC = \frac{1}{2}(180^{\circ} - \angle B - \angle C)$,
$\angle CAD = 90^{\circ} - \angle C$,
$\therefore \angle DAE = \angle CAE - \angle CAD = \frac{1}{2}(180^{\circ} - \angle B - \angle C) - (90^{\circ} - \angle C) = \frac{1}{2}(\angle C - \angle B)$.
(1)$\because \angle B = 30^{\circ}, \angle C = 50^{\circ}$,
$\therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 100^{\circ}$.
$\because AE$平分$\angle BAC$,
$\therefore \angle CAE = \frac{1}{2}\angle BAC = 50^{\circ}$.
$\because AD \perp BC, \angle C = 50^{\circ}$,
$\therefore \angle DAC = 90^{\circ} - 50^{\circ} = 40^{\circ}$,
$\therefore \angle DAE = \angle CAE - \angle CAD = 50^{\circ} - 40^{\circ} = 10^{\circ}$.
(2)$\angle DAE = \frac{1}{2}(\angle C - \angle B)$.理由如下:
$\because AD,AE$分别是$\triangle ABC$的高和角平分线,
答案
$\therefore \angle CAE = \frac{1}{2}\angle BAC = \frac{1}{2}(180^{\circ} - \angle B - \angle C)$,
$\angle CAD = 90^{\circ} - \angle C$,
$\therefore \angle DAE = \angle CAE - \angle CAD = \frac{1}{2}(180^{\circ} - \angle B - \angle C) - (90^{\circ} - \angle C) = \frac{1}{2}(\angle C - \angle B)$.
14. [新考法·过程性探究活动] 在数学课上,张老师引导大家探究角平分线的夹角问题。在 $\triangle ABC$ 中,$\angle ABC$ 与 $\angle ACB$ 的平分线相交于点 $P$。
【问题研究】
(1)①如图 1,若 $\angle ABC = 50^{\circ}$,$\angle ACB = 70^{\circ}$,则 $\angle BPC =$
②猜测 $\angle BPC$ 与 $\angle A$ 之间的数量关系,并证明;
【问题延伸】
(2)如图 2,作 $\triangle ABC$ 的外角 $\angle CBM$,$\angle BCN$ 的平分线,相交于点 $Q$,则 $\angle Q$ 与 $\angle BPC$ 之间的数量关系为
【拓展应用】
(3)如图 3,在(2)的条件下,延长线段 $BP$,$QC$,相交于点 $E$,在 $\triangle BQE$ 中,当 $\angle E$ 与 $\angle Q$ 两锐角存在 $3$ 倍的数量关系时,求 $\angle A$ 的度数。
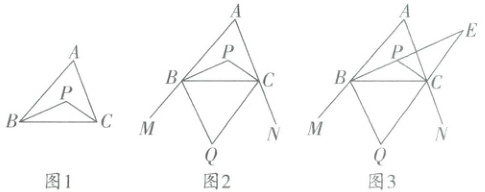
【问题研究】
(1)①如图 1,若 $\angle ABC = 50^{\circ}$,$\angle ACB = 70^{\circ}$,则 $\angle BPC =$
$120^{\circ}$
;②猜测 $\angle BPC$ 与 $\angle A$ 之间的数量关系,并证明;
【问题延伸】
(2)如图 2,作 $\triangle ABC$ 的外角 $\angle CBM$,$\angle BCN$ 的平分线,相交于点 $Q$,则 $\angle Q$ 与 $\angle BPC$ 之间的数量关系为
$\angle Q = 180^{\circ} - \angle BPC$
;【拓展应用】
(3)如图 3,在(2)的条件下,延长线段 $BP$,$QC$,相交于点 $E$,在 $\triangle BQE$ 中,当 $\angle E$ 与 $\angle Q$ 两锐角存在 $3$ 倍的数量关系时,求 $\angle A$ 的度数。

答案:
14.解:
(1)①$120^{\circ}$
②猜想$\angle BPC = 90^{\circ} + \frac{1}{2}\angle A$.证明如下:
$\because \angle A + \angle ACB + \angle ABC = 180^{\circ}$,
$\therefore \angle ACB + \angle ABC = 180^{\circ} - \angle A$.
$\because BP,CP$分别是$\angle ABC$和$\angle ACB$的平分线,
$\therefore \angle PBC = \frac{1}{2}\angle ABC, \angle BCP = \frac{1}{2}\angle ACB$.
$\because \angle PBC + \angle BCP + \angle BPC = 180^{\circ}$,
$\therefore \angle BPC = 180^{\circ} - \angle PBC - \angle BCP$
$= 180^{\circ} - \frac{1}{2}\angle ABC - \frac{1}{2}\angle ACB$
$= 180^{\circ} - \frac{1}{2}(\angle ABC + \angle ACB)$
$= 180^{\circ} - \frac{1}{2}(180^{\circ} - \angle A)$
$= 90^{\circ} + \frac{1}{2}\angle A$.
(2)$\angle Q = 180^{\circ} - \angle BPC$
(3)$\because BP$是$\angle ABC$的平分线,$BQ$是$\angle CBM$的平分线,
$\therefore \angle PBC = \frac{1}{2}\angle ABC, \angle CBQ = \frac{1}{2}\angle CBM$.
$\because \angle ABC + \angle CBM = 180^{\circ}$,
$\therefore \angle PBC + \angle CBQ = \frac{1}{2}(\angle ABC + \angle CBM) = 90^{\circ}$,
$\therefore \angle QBE = \angle PBC + \angle CBQ = 90^{\circ}$,
$\therefore \angle E + \angle Q = 90^{\circ}$.
由
(2)知$\angle Q = 180^{\circ} - \angle BPC = 90^{\circ} - \frac{1}{2}\angle A$,
$\therefore \angle E = \frac{1}{2}\angle A$.
当$\angle Q = 3\angle E$时,$90^{\circ} - \frac{1}{2}\angle A = 3 × \frac{1}{2}\angle A$,
解得$\angle A = 45^{\circ}$.
当$\angle E = 3\angle Q$时,$3(90^{\circ} - \frac{1}{2}\angle A) = \frac{1}{2}\angle A$,
解得$\angle A = 135^{\circ}$.
综上所述,$\angle A$的度数为$45^{\circ}$或$135^{\circ}$.
(1)①$120^{\circ}$
②猜想$\angle BPC = 90^{\circ} + \frac{1}{2}\angle A$.证明如下:
$\because \angle A + \angle ACB + \angle ABC = 180^{\circ}$,
$\therefore \angle ACB + \angle ABC = 180^{\circ} - \angle A$.
$\because BP,CP$分别是$\angle ABC$和$\angle ACB$的平分线,
$\therefore \angle PBC = \frac{1}{2}\angle ABC, \angle BCP = \frac{1}{2}\angle ACB$.
$\because \angle PBC + \angle BCP + \angle BPC = 180^{\circ}$,
$\therefore \angle BPC = 180^{\circ} - \angle PBC - \angle BCP$
$= 180^{\circ} - \frac{1}{2}\angle ABC - \frac{1}{2}\angle ACB$
$= 180^{\circ} - \frac{1}{2}(\angle ABC + \angle ACB)$
$= 180^{\circ} - \frac{1}{2}(180^{\circ} - \angle A)$
$= 90^{\circ} + \frac{1}{2}\angle A$.
(2)$\angle Q = 180^{\circ} - \angle BPC$
(3)$\because BP$是$\angle ABC$的平分线,$BQ$是$\angle CBM$的平分线,
$\therefore \angle PBC = \frac{1}{2}\angle ABC, \angle CBQ = \frac{1}{2}\angle CBM$.
$\because \angle ABC + \angle CBM = 180^{\circ}$,
$\therefore \angle PBC + \angle CBQ = \frac{1}{2}(\angle ABC + \angle CBM) = 90^{\circ}$,
$\therefore \angle QBE = \angle PBC + \angle CBQ = 90^{\circ}$,
$\therefore \angle E + \angle Q = 90^{\circ}$.
由
(2)知$\angle Q = 180^{\circ} - \angle BPC = 90^{\circ} - \frac{1}{2}\angle A$,
$\therefore \angle E = \frac{1}{2}\angle A$.
当$\angle Q = 3\angle E$时,$90^{\circ} - \frac{1}{2}\angle A = 3 × \frac{1}{2}\angle A$,
解得$\angle A = 45^{\circ}$.
当$\angle E = 3\angle Q$时,$3(90^{\circ} - \frac{1}{2}\angle A) = \frac{1}{2}\angle A$,
解得$\angle A = 135^{\circ}$.
综上所述,$\angle A$的度数为$45^{\circ}$或$135^{\circ}$.
查看更多完整答案,请扫码查看


