《2025年有一套初中各地市期末真题八年级数学上册人教版》

23. [学科素养·推理能力](本小题12分)【问题初探】
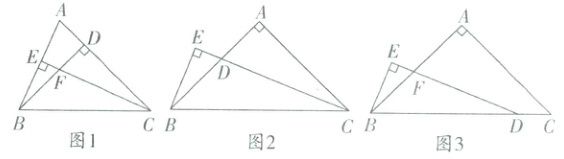
(1) 在数学社团活动中，李老师给同学们出了这样一道题：如图1，在$\triangle ABC$中，高$BD,CE$交于点$F$，且$BD = CD$，试说明$FC,AB$有怎样的数量关系.
小明经过思考，说出了他的方法：根据已知条件，易证$\triangle ABD\cong\triangle FCD$，从而得出$FC = AB$.
小明证明$\triangle ABD\cong\triangle FCD$的依据可能是 ________ (填序号)；
①SSS
②ASA
③HL
④SAS
【引导发现】
(2) 老师看同学们的兴致很高，又出了一道题：如图2，在$\triangle ABC$中，$AB = AC,\angle A = 90^{\circ}$，$CD$平分$\angle ACB$，$BE\perp CD$，垂足$E$在$CD$的延长线上.
①填空：$\angle ABE = $ ________ $^{\circ}$；
②判断线段$BE$与$CD$的数量关系，并写出证明过程；
【拓展延伸】
(3) $\triangle ABC$中，$AB = AC,\angle A = 90^{\circ}$，如图3，点$D$在线段$BC$上，$BE\perp ED$于点$E$，$DE$交$AB$于点$F$，且$\angle ABE=\angle EDB$，请直接写出$BE$和$DF$的数量关系.

答案：
23.解：
(1)②
(2)①22.5
②CD = 2BE。证明如下：
延长BE，交CA的延长线于点F。
∵CD平分∠ACB，
∴∠FCE = ∠BCE。
在△CEF和△CEB中，$\begin{cases}∠FCE = ∠BCE,\\CE = CE,\\∠CEF = ∠CEB = 90°,\end{cases}$
∴△CEF ≌ △CEB(ASA)，
∴FE = BE = $\frac{1}{2}$BF。
∵∠DAC = ∠CEF = ∠BAF = 90°，
∴∠ACD + ∠F = ∠ABF + ∠F = 90°，
∴∠ACD = ∠ABF。
在△ACD和△ABF中，$\begin{cases}∠ACD = ∠ABF,\\AC = AB,\\∠CAD = ∠BAF = 90°,\end{cases}$
∴△ACD ≌ △ABF(ASA)，
∴CD = BF，
∴CD = 2BE。
(3)BE = $\frac{1}{2}$DF。
【解题思路】如图，过点D作DG//AC，交BE的延长线于点G，与AF交于点H。

∵DG//AC，
∴∠BHD = ∠A = 90°。
∵BE⊥ED，
∴∠BED = 90°，
∴∠BED = ∠BHD。
∵∠EFB = ∠HFD，
∴∠EBF = ∠HDF。
∵∠ABE = ∠EDG，∠ABE = ∠EDB，
∴∠EDB = ∠EDG = $\frac{1}{2}$∠C。
∵AB = AC，∠BAC = 90°，
∴∠C = ∠ABC = 45°。
∵DG//AC，
∴∠GDB = ∠C = 45°，
∴∠GDB = ∠ABC = 45°，
∴BH = DH。
在△BGH和△DFH中，$\begin{cases}∠HBG = ∠HDF,\\BH = DH,\\∠BHG = ∠DHF = 90°,\end{cases}$
∴△BGH ≌ △DFH(ASA)，
∴BG = DF。
在△BDE和△GDE中，$\begin{cases}∠BDE = ∠GDE,\\DE = DE,\\∠BED = ∠GED = 90°,\end{cases}$
∴△BDE ≌ △GDE(ASA)，
∴BE = GE。
∴BE = $\frac{1}{2}$BG = $\frac{1}{2}$DF。