《2025年有一套初中各地市期末真题八年级数学上册人教版》

9. 我们定义：若一个整式能表示成$a^{2}+b^{2}$($a,b$是整式)的形式，则称这个整式为“完全式”. 例如：因为$M = x^{2}+2xy + 2y^{2}=(x + y)^{2}+y^{2}$($x,y$是整式)，所以$M$为“完全式”. 若$S = x^{2}+4y^{2}-8x + 12y + k$($x,y$是整式，$k$为常数)为“完全式”，则$k$的值为 (B)
A.26
B.25
C.24
D.23

答案： 9.B

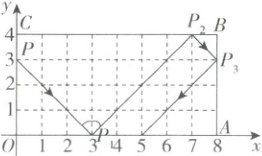
10. 小静同学观察台球比赛，从中受到启发，抽象成数学问题如下：如图，已知长方形$OABC$，小球$P$从$(0,3)$出发，沿如图所示的方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，第一次碰到长方形的边时的位置为$P_{1}(3,0)$，当小球$P$第2026次碰到长方形的边时，若不考虑阻力，点$P_{2026}$的坐标是 (D)

A.$(1,4)$
B.$(7,4)$
C.$(0,3)$
D.$(5,0)$

答案： 10.D 【解析】因为点P₁的坐标为(3,0)，根据点P的运动方式，结合反射角等于入射角可知，点P₂的坐标为(7,4)，点P₃的坐标为(8,3)，点P₄的坐标为(5,0)，点P₅的坐标为(1,4)，点P₆的坐标为(0,3)，点P₇的坐标为(3,0)，……，由此可见，点P每反弹6次，点的坐标循环出现。因为2026÷6 = 337……4，所以点P₂₀₂₆的坐标为(5,0)。故选：D。

11. 工程建筑中经常采用三角形的结构，如屋顶钢架，其中的数学道理是 三角形具有稳定性.

答案： 11.三角形具有稳定性

12. 若$x$满足$(x - 2)^{x + 1}=1$，则整数$x$的值为 -1或3或1.

答案： 12. -1或3或1

13. 长、宽分别为$a,b$的长方形，其周长为24，面积为32，则$a^{2}b + ab^{2}$的值为 384.

答案： 13.384

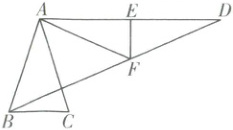
14. 如图，在$\triangle ABC$中，$AB = AC,\angle BAC = 36^{\circ}$，过点$A$作$AD// BC$，连接$BD$，作线段$AD$的垂直平分线$EF$交$AD$于点$E$，交$BD$于点$F$，连接$AF$，若$AF = AB$，则$\angle D = $ 24 $^{\circ}$.

答案： 14.24

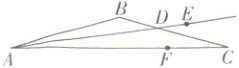
15. 如图，在$\triangle ABC$中，$BC = BA = 36,\angle C = 15^{\circ}$，$AD$平分$\angle BAC$，$E,F$分别是射线$AD$和线段$AC$上的动点，连接$CE,EF$，则$CE + EF$的最小值为 18.

答案： 15.18 【解析】作点F关于AD的对称点M，作AB边上的高CP，连接CM。
∵AD平分∠BAC，
∴点M必在AB上。
∵点F关于AD的对称点为M，
∴ME = EF。
∴CE + EF = CE + EM ≥ MC ≥ PC。
当C，E，M三点共线，且CM⊥AB时，CE + EF的值最小，最小值为CP的长。
∵BC = BA = 36，∠C = 15°，
∴∠BAC = ∠BCA = 15°。
∴∠PBC = ∠BAC + ∠BCA = 30°，
∴CP = $\frac{1}{2}$BC = 18。
即CE + EF的最小值为18。故答案为：18。