2025年有一套初中各地市期末真题八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年有一套初中各地市期末真题八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 如图是应用 DeepSeek 公司研发的一个 AI 模型画出的图形,在 $\triangle ABF$ 中,顶点 $B$ 的对边是
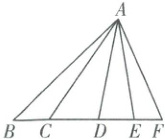
AF
。
答案:
8.AF
9. 如图,$D$ 是 $\triangle ABC$ 的边 $BC$ 上任意一点,$E$ 是线段 $AD$ 的中点,若 $S_{\triangle ABC} = 12$,则阴影部分的面积为

6
。
答案:
9.6
10. 如图,已知 $\angle A = \alpha$,$\angle ACD$ 是 $\triangle ABC$ 的外角,$\angle ABC$ 的平分线与 $\angle ACD$ 的平分线相交于点 $A_1$,得 $\angle A_1$;若 $\angle A_1BC$ 的平分线与 $\angle A_1CD$ 的平分线相交于点 $A_2$,得 $\angle A_2$;$·s$;$\angle A_{2024}BC$ 的平分线与 $\angle A_{2024}CD$ 的平分线相交于点 $A_{2025}$,得 $\angle A_{2025}$。则 $\angle A_{2025} =$
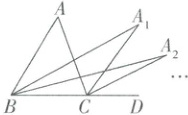
$\frac{1}{2^{2025}}\alpha$
。(用含 $\alpha$ 的式子表示)
答案:
10. $\frac{1}{2^{2025}}\alpha$【解析】$\because BA_1$ 平分$\angle ABC,CA_1$ 平分$\angle ACD$,
$\therefore \angle A_1BC = \frac{1}{2}\angle ABC, \angle A_1CD = \frac{1}{2}\angle ACD$.
$\because \angle ACD = \angle A + \angle ABC, \angle A_1CD = \angle A_1 + \angle A_1BC$,
$\therefore \frac{1}{2}\angle A + \frac{1}{2}\angle ABC = \angle A_1 + \frac{1}{2}\angle ABC$,
$\therefore \angle A_1 = \frac{1}{2}\angle A = \frac{1}{2}\alpha$.
同理可得$\angle A_2 = \frac{1}{2}\angle A_1 = \frac{1}{4}\angle A$,
$\angle A_3 = \frac{1}{2}\angle A_2 = \frac{1}{8}\angle A$,
$·s$
$\therefore \angle A_{2025} = \frac{1}{2}\angle A_{2024} = \frac{1}{2^{2025}}\angle A = \frac{1}{2^{2025}}\alpha$.
故答案为:$\frac{1}{2^{2025}}\alpha$.
$\therefore \angle A_1BC = \frac{1}{2}\angle ABC, \angle A_1CD = \frac{1}{2}\angle ACD$.
$\because \angle ACD = \angle A + \angle ABC, \angle A_1CD = \angle A_1 + \angle A_1BC$,
$\therefore \frac{1}{2}\angle A + \frac{1}{2}\angle ABC = \angle A_1 + \frac{1}{2}\angle ABC$,
$\therefore \angle A_1 = \frac{1}{2}\angle A = \frac{1}{2}\alpha$.
同理可得$\angle A_2 = \frac{1}{2}\angle A_1 = \frac{1}{4}\angle A$,
$\angle A_3 = \frac{1}{2}\angle A_2 = \frac{1}{8}\angle A$,
$·s$
$\therefore \angle A_{2025} = \frac{1}{2}\angle A_{2024} = \frac{1}{2^{2025}}\angle A = \frac{1}{2^{2025}}\alpha$.
故答案为:$\frac{1}{2^{2025}}\alpha$.
11. 如图,$\triangle ABC$ 的面积是 $15$,$AB = AC = 6$,$O$ 是边 $BC$ 上任意一点(不与点 $B$,$C$ 重合),$OD \perp AB$ 于点 $D$,$OE \perp AC$ 于点 $E$,设 $OD = a$,$OE = b$,则代数式 $a + b$ 的值是
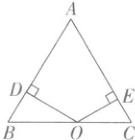
11.5
。
答案:
11.5
12. 如图,在 $\triangle ABC$ 中,点 $D$ 在 $BC$ 边上,连接 $AD$,$\angle ADB = \angle ABD$。$BE$ 是 $\triangle ABD$ 中 $AD$ 边上的高线,延长 $BE$ 交 $AC$ 于点 $F$。设 $\angle ABC = \alpha$,$\angle ACB = \beta$。
(1)当 $\alpha = 70^{\circ}$ 时,$\angle ABF$ 的度数为
(2)求 $\angle AFB$ 的度数(用含 $\alpha$,$\beta$ 的式子表示);
(3)若 $\angle AFB = \angle BAF$,求 $\beta$ 的值。

(1)当 $\alpha = 70^{\circ}$ 时,$\angle ABF$ 的度数为
50°
;(2)求 $\angle AFB$ 的度数(用含 $\alpha$,$\beta$ 的式子表示);
(3)若 $\angle AFB = \angle BAF$,求 $\beta$ 的值。

答案:
12.解:
(1)$50^{\circ}$
(2)$\because \angle ADB = \angle ABD, \angle ABC = \alpha$.
$\therefore \angle ADB = \angle ABD = \alpha$.
$\because BE$是$\triangle ABD$中$AD$边上的高线,
$\therefore BE \perp AD$,即$\angle BED = 90^{\circ}$,
$\therefore \angle DBE = 90^{\circ} - \angle BDE = 90^{\circ} - \alpha$,
$\therefore \angle AFB = \angle CBF + \angle ACB = 90^{\circ} - \alpha + \beta$.
(3)$\because \angle AFB = \angle BAF, \angle AFB = 90^{\circ} - \alpha + \beta$,
$\therefore \angle BAF = 90^{\circ} - \alpha + \beta$.
$\because \angle BAF + \angle ABC + \angle ACB = 180^{\circ}$,
$\therefore 90^{\circ} - \alpha + \beta + \alpha + \beta = 180^{\circ}$,
$\therefore \beta = 45^{\circ}$.
(1)$50^{\circ}$
(2)$\because \angle ADB = \angle ABD, \angle ABC = \alpha$.
$\therefore \angle ADB = \angle ABD = \alpha$.
$\because BE$是$\triangle ABD$中$AD$边上的高线,
$\therefore BE \perp AD$,即$\angle BED = 90^{\circ}$,
$\therefore \angle DBE = 90^{\circ} - \angle BDE = 90^{\circ} - \alpha$,
$\therefore \angle AFB = \angle CBF + \angle ACB = 90^{\circ} - \alpha + \beta$.
(3)$\because \angle AFB = \angle BAF, \angle AFB = 90^{\circ} - \alpha + \beta$,
$\therefore \angle BAF = 90^{\circ} - \alpha + \beta$.
$\because \angle BAF + \angle ABC + \angle ACB = 180^{\circ}$,
$\therefore 90^{\circ} - \alpha + \beta + \alpha + \beta = 180^{\circ}$,
$\therefore \beta = 45^{\circ}$.
查看更多完整答案,请扫码查看


