《2025年天星教育试题调研数学第10辑》

在四棱锥 $ P - ABCD $ 中，$ AB = AD = \sqrt{10} $，$ CB = CD = 5 $，$ \angle BAD = 90^{\circ} $，$ PB = 4 $，$ PC = 3 $。
(1) 证明：$ PB $ 与 $ CD $ 不垂直。
(2) 已知 $ \triangle PBC $ 内部点 $ Q $ 满足四棱锥 $ Q - ABCD $ 与三棱锥 $ Q - PAD $ 的体积相等。
(i) 求 $ PQ $ 长的最小值。
(ii) 在 (i) 的条件下求三棱锥 $ Q - PAD $ 体积的最大值。

答案：

解析
(1) 作出四棱锥 $ P - ABCD $，如图 1，
在 $ \triangle PBC $ 中，$ PB^{2} + PC^{2} = 16 + 9 = 25 = BC^{2} $，所以 $ PB \perp PC $。
假设 $ PB \perp CD $，则由 $ CD \cap PC = P $，$ CD $，$ PC \subset $ 平面 $ PCD $，得 $ PB \perp $ 平面 $ PCD $，
【障碍速通】直接证明两异面直线不垂直较复杂，故利用反证法，先假设两直线垂直，推出矛盾即可
又 $ PD \subset $ 平面 $ PCD $，所以 $ PB \perp PD $。
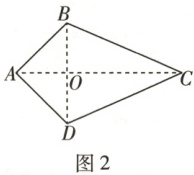
作出平面四边形 $ ABCD $，如图 2，连接 $ AC $，$ BD $，设 $ AC $ 与 $ BD $ 交于点 $ O $，
易知 $ AC \perp BD $，且 $ O $ 为 $ BD $ 的中点，则由 $ AB = AD = \sqrt{10} $，$ \angle BAD = 90^{\circ} $，
得 $ BD = 2BO = 2 × \sqrt{10} × \frac{\sqrt{2}}{2} = 2\sqrt{5} $。
在 $ Rt \triangle PBD $ 中，$ PD = \sqrt{BD^{2} - PB^{2}} = \sqrt{20 - 16} = 2 $，
在 $ \triangle PCD $ 中，$ PC + PD = 3 + 2 = 5 = DC $，这不可能，故假设错误，$ PB $ 与 $ CD $ 不垂直。
(2)(i) 在平面四边形 $ ABCD $ 中，易得 $ AO = \sqrt{5} $，$ CO = 2\sqrt{5} $，$ S_{\triangle OBC} = S_{\triangle ODC} = 2S_{\triangle OAB} = 2S_{\triangle OAD} = 5 $，
如图 1，设平面 $ QAD $ 与平面 $ PBC $ 的交线为 $ MN $，
由 $ V_{Q - ABCD} = V_{Q - PAD} $，得 $ 2V_{Q - ACD} = V_{Q - PAD} $，得 $ 2V_{C - QAD} = V_{P - QAD} $，
所以 $ P $ 到平面 $ QAD $ 的距离是 $ C $ 到平面 $ QAD $ 的距离的 $ 2 $ 倍，所以 $ \frac{PM}{MC} = \frac{2}{1} $。
由 $ V_{Q - ABCD} = V_{Q - PAD} $，得 $ 3V_{Q - ABD} = V_{Q - PAD} $，得 $ 3V_{B - QAD} = V_{P - QAD} $，
所以 $ P $ 到平面 $ QAD $ 的距离是 $ B $ 到平面 $ QAD $ 的距离的 $ 3 $ 倍，所以 $ \frac{PN}{NB} = \frac{3}{1} $。
【障碍速通】通过面积关系先将四棱锥的体积转化为三棱锥的体积，再结合等体积法更换底面，从而将体积的比例关系转化为线段长的比例关系
所以 $ Q $ 的轨迹是线段 $ MN $，其中 $ M $ 为 $ PC $ 的三等分点，$ N $ 为 $ PB $ 的四等分点，则 $ PM = 2 $，$ PN = 3 $。
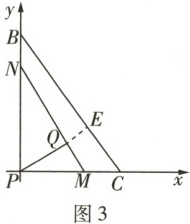
如图 3，当 $ PQ \perp MN $ 时，$ PQ $ 最短，
【技法速通】降维处理，将空间中的线段放在平面图形中求解
由
(1) 知 $ \triangle PBC $ 为直角三角形，$ MN = \sqrt{3^{2} + 2^{2}} = \sqrt{13} $，则由等面积法
得 $ PQ · MN = PM · PN $，$ PQ = \frac{PM × PN}{MN} = \frac{2 × 3}{\sqrt{13}} = \frac{6\sqrt{13}}{13} $，
所以 $ PQ $ 长的最小值为 $ \frac{6\sqrt{13}}{13} $。
(ii) 过点 $ Q $ 作 $ QE \perp BC $ 于 $ E $，过点 $ Q $ 作 $ QF \perp $ 平面 $ ABCD $ 于 $ F $，
则 $ QF \leq QE $。
如图 3，以 $ P $ 为坐标原点，直线 $ PC $，$ PB $ 分别为 $ x $ 轴，$ y $ 轴建立平面直角坐标系，则 $ Q(\frac{18}{13}, \frac{12}{13}) $，
【技法速通】由于平面四边形 $ BNMC $ 为不规则四边形，利用垂直的性质求解较复杂，故结合 $ PB \perp PC $ 建立平面直角坐标系，利用坐标求解
直线 $ BC $ 的方程为 $ \frac{x}{3} + \frac{y}{4} = 1 $，即 $ 4x + 3y - 12 = 0 $，
则点 $ Q $ 到直线 $ BC $ 的距离 $ QE = \frac{|4 × \frac{18}{13} + 3 × \frac{12}{13} - 12|}{5} = \frac{48}{65} $，所以 $ QF \leq \frac{48}{65} $。
在平面四边形 $ ABCD $ 中，$ AC = 3\sqrt{5} $，所以 $ S_{四边形ABCD} = \frac{1}{2}AC × BD = 15 $，
则 $ V_{Q - PAD} = V_{Q - ABCD} = \frac{1}{3} × S_{四边形ABCD} × QF \leq \frac{1}{3} × 15 × \frac{48}{65} \leq \frac{48}{13} $。
所以三棱锥 $ Q - PAD $ 体积的最大值为 $ \frac{48}{13} $。