2025年天星教育试题调研化学第9辑
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天星教育试题调研化学第9辑 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
第3题 反应速率平衡图像绘制问题
热考指数 ★★★★★
原创预测 一碳化学是指以分子中只含一个碳原子的化合物 (如 $ {CH_{4}} $、$ {CO} $、$ {CO_{2}} $ 等) 为初始反应物,合成一系列重要的化工原料和燃料的化学。
回答下列问题:
(1) 将一氧化碳转化为有机物再利用能有效助力碳达峰和碳中和。已知:

则反应 $ {CO_{2}(g) + 3H_{2}(g){<=>[][]}CH_{3}OH(g) + H_{2}O(g)} $ 的焓变 $ \Delta H = $ (用含 $ \Delta H_{1} $、$ \Delta H_{2} $ 的式子表示)。
(2) 一定温度下,反应 $ {CO(g) + H_{2}O(g){<=>[][]}CO_{2}(g) + H_{2}(g)} $ 的平衡常数 $ K = 1.0 $,该温度下,向 $ 2 \ L $ 固定容积的密闭容器中加入 $ {CO(g)} $ 和 $ {H_{2}O(g)} $ 各 $ 1 \ mol $,$ 5 \ min $ 后反应达到平衡,则 $ 0~5 \ min $ 内用 $ {H_{2}} $ 表示的平均反应速率为 $ mol · L^{-1} · min^{-1} $,$ {CO} $ 的转化率为 。
(3) 合成气 ($ {CO} $ 和 $ {H_{2}} $) 在工业上有着广泛的应用,一种制备合成气的原理为 (ⅰ) $ {CO_{2}(g) + CH_{4}(g){<=>[][]}2CO(g) + 2H_{2}(g)} $ $ \Delta H = +245.4 \ kJ · mol^{-1} $,该反应进行时可能伴随副反应 (ⅱ) $ {CO_{2}(g) + H_{2}(g){<=>[][]}CO(g) + H_{2}O(g)} $ $ \Delta H = +41 \ kJ · mol^{-1} $。
① 反应 (ⅰ) 在高温下能够自发进行的原因是 。
② 在图 1 所示甲、乙两容器中均充入等物质的量的 $ {CH_{4}} $ 和 $ {CO_{2}} $,使甲、乙两容器初始容积相等,在相同温度下只发生反应 (ⅰ),并维持反应过程中温度不变。已知甲容器中 $ {CH_{4}} $ 的转化率随时间的变化关系如图 2 所示,请在图 2 中画出乙容器中 $ {CH_{4}} $ 的转化率随时间变化关系的图像。
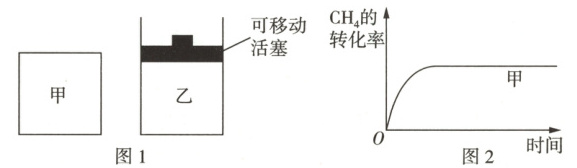
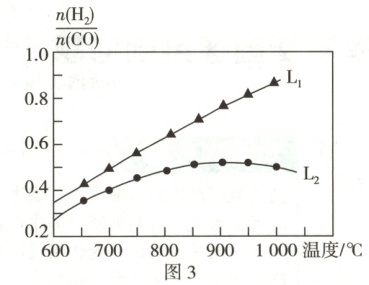
③ 在密闭容器中加入一定量的 $ {CH_{4}} $ 和 $ {CO_{2}} $,发生反应 (ⅰ)(ⅱ),测得在不同投料比 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $ 下,平衡时 $ \dfrac{n({H_{2}})}{n({CO})} $ 随温度的变化如图 3 所示。比较图 3 中 $ {L_{1}} $、$ {L_{2}} $ 对应的投料比 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $:$ {L_{1}} $ (填“$ > $”或“$ < $”) $ {L_{2}} $。曲线 $ {L_{2}} $ 中,当温度高于 $ 900 \ ^{\circ}C $,$ \dfrac{n({H_{2}})}{n({CO})} $ 减小的原因可能是 。
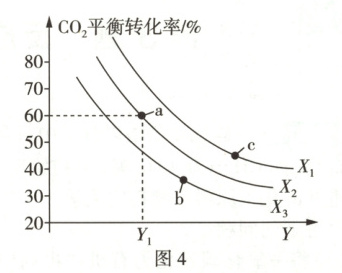
(4) 我国科学家利用二氧化碳催化氢化的方法合成甲酸的研究取得了很大的进展,反应原理为 Ⅰ. $ {CO_{2}(g) + H_{2}(g){<=>[][]}HCOOH(g)} $ $ \Delta H_{1} = -30.9 \ kJ · mol^{-1} $,同时伴随副反应 Ⅱ. $ {CO_{2}(g) + H_{2}(g){<=>[][]}CO(g) + H_{2}O(g)} $ $ \Delta H_{2} = +41 \ kJ · mol^{-1} $。某兴趣小组向密闭容器内加入 $ 1 \ mol \ {CO_{2}(g)} $ 和 $ 1 \ mol \ {H_{2}(g)} $,发生上述反应,测得 $ {CO_{2}} $ 的平衡转化率随
温度和压强 ($ MPa $) 的变化关系如图 4 所示。
① $ Y $ 表示 (填“温度”或“压强”)。
② 图中 $ a $、$ b $、$ c $ 三点对应的反应 Ⅰ 的化学平衡常数 $ K $ 由大到小的顺序为 。
③ $ a $ 点所处条件下,平衡时容器内 $ p({HCOOH}) = 5p({CO}) $,则反应 Ⅰ 的 $ K_{p} = $ 。
热考指数 ★★★★★
原创预测 一碳化学是指以分子中只含一个碳原子的化合物 (如 $ {CH_{4}} $、$ {CO} $、$ {CO_{2}} $ 等) 为初始反应物,合成一系列重要的化工原料和燃料的化学。
回答下列问题:
(1) 将一氧化碳转化为有机物再利用能有效助力碳达峰和碳中和。已知:

则反应 $ {CO_{2}(g) + 3H_{2}(g){<=>[][]}CH_{3}OH(g) + H_{2}O(g)} $ 的焓变 $ \Delta H = $ (用含 $ \Delta H_{1} $、$ \Delta H_{2} $ 的式子表示)。
(2) 一定温度下,反应 $ {CO(g) + H_{2}O(g){<=>[][]}CO_{2}(g) + H_{2}(g)} $ 的平衡常数 $ K = 1.0 $,该温度下,向 $ 2 \ L $ 固定容积的密闭容器中加入 $ {CO(g)} $ 和 $ {H_{2}O(g)} $ 各 $ 1 \ mol $,$ 5 \ min $ 后反应达到平衡,则 $ 0~5 \ min $ 内用 $ {H_{2}} $ 表示的平均反应速率为 $ mol · L^{-1} · min^{-1} $,$ {CO} $ 的转化率为 。
(3) 合成气 ($ {CO} $ 和 $ {H_{2}} $) 在工业上有着广泛的应用,一种制备合成气的原理为 (ⅰ) $ {CO_{2}(g) + CH_{4}(g){<=>[][]}2CO(g) + 2H_{2}(g)} $ $ \Delta H = +245.4 \ kJ · mol^{-1} $,该反应进行时可能伴随副反应 (ⅱ) $ {CO_{2}(g) + H_{2}(g){<=>[][]}CO(g) + H_{2}O(g)} $ $ \Delta H = +41 \ kJ · mol^{-1} $。
① 反应 (ⅰ) 在高温下能够自发进行的原因是 。
② 在图 1 所示甲、乙两容器中均充入等物质的量的 $ {CH_{4}} $ 和 $ {CO_{2}} $,使甲、乙两容器初始容积相等,在相同温度下只发生反应 (ⅰ),并维持反应过程中温度不变。已知甲容器中 $ {CH_{4}} $ 的转化率随时间的变化关系如图 2 所示,请在图 2 中画出乙容器中 $ {CH_{4}} $ 的转化率随时间变化关系的图像。

③ 在密闭容器中加入一定量的 $ {CH_{4}} $ 和 $ {CO_{2}} $,发生反应 (ⅰ)(ⅱ),测得在不同投料比 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $ 下,平衡时 $ \dfrac{n({H_{2}})}{n({CO})} $ 随温度的变化如图 3 所示。比较图 3 中 $ {L_{1}} $、$ {L_{2}} $ 对应的投料比 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $:$ {L_{1}} $ (填“$ > $”或“$ < $”) $ {L_{2}} $。曲线 $ {L_{2}} $ 中,当温度高于 $ 900 \ ^{\circ}C $,$ \dfrac{n({H_{2}})}{n({CO})} $ 减小的原因可能是 。


(4) 我国科学家利用二氧化碳催化氢化的方法合成甲酸的研究取得了很大的进展,反应原理为 Ⅰ. $ {CO_{2}(g) + H_{2}(g){<=>[][]}HCOOH(g)} $ $ \Delta H_{1} = -30.9 \ kJ · mol^{-1} $,同时伴随副反应 Ⅱ. $ {CO_{2}(g) + H_{2}(g){<=>[][]}CO(g) + H_{2}O(g)} $ $ \Delta H_{2} = +41 \ kJ · mol^{-1} $。某兴趣小组向密闭容器内加入 $ 1 \ mol \ {CO_{2}(g)} $ 和 $ 1 \ mol \ {H_{2}(g)} $,发生上述反应,测得 $ {CO_{2}} $ 的平衡转化率随
温度和压强 ($ MPa $) 的变化关系如图 4 所示。
① $ Y $ 表示 (填“温度”或“压强”)。
② 图中 $ a $、$ b $、$ c $ 三点对应的反应 Ⅰ 的化学平衡常数 $ K $ 由大到小的顺序为 。
③ $ a $ 点所处条件下,平衡时容器内 $ p({HCOOH}) = 5p({CO}) $,则反应 Ⅰ 的 $ K_{p} = $ 。
答案:
解析
(1) 结合盖斯定律可知,目标反应 $ = $ 反应ⅰ $ + $ 反应ⅱ,则反应 $ {CO_{2}(g) + 3H_{2}(g){<=>[][]}CH_{3}OH(g) + H_{2}O(g)} $ 的焓变 $ \Delta H = \Delta H_{1} + \Delta H_{2} $。
(2) 设达到平衡时 $ {CO} $ 的转化量为 $ x \ mol $,可列三段式:
$ \begin{array}{cccccc} & {CO(g)} & + & {H_{2}O(g)} & {<=>[][]} & {CO_{2}(g)} & + & {H_{2}(g)} \\ 起始量/mol & 1 & & 1 & & 0 & & 0 \\ 转化量/mol & x & & x & & x & & x \\ 平衡量/mol & 1 - x & & 1 - x & & x & & x \end{array} $
则该反应的平衡常数 $ K = \dfrac{x^{2}}{(1 - x)^{2}} = 1.0 $,解得 $ x = 0.5 $,则平衡时,$ n({CO}) = n({H_{2}O}) = $
【解题突破】对于反应前后气体分子数不变的反应,可直接用物质的量代替物质的量浓度、分压来计算 $ K_{c} $、$ K_{p} $。
$ n({CO_{2}}) = n({H_{2}}) = 0.5 \ mol $;$ {CO(g)} $ 的转化率为 $ \dfrac{0.5 \ mol}{1 \ mol} × 100\% = 50\% $,$ 0~5 \ min $ 内,$ {H_{2}} $ 的平均反应速率为 $ \dfrac{0.5 \ mol}{2 \ L × 5 \ min} = 0.05 \ mol · L^{-1} · min^{-1} $。
(3) ① 反应 (ⅰ) 为反应前后气体分子数增大的反应,$ \Delta S > 0 $,又 $ \Delta H > 0 $,在高温条件下,有 $ \Delta H - T\Delta S < 0 $,此时该反应能够自发进行。
② 根据题图 1 可知,甲容器中反应条件是恒温恒容,乙容器中反应条件是恒温恒压。反应开始时甲、乙两容器初始容积相等,在相同温度下发生反应 (ⅰ)$ {CH_{4}(g) + CO_{2}(g){<=>[][]}2CO(g) + 2H_{2}(g)} $ $ \Delta H = +245.4 \ kJ · mol^{-1} $;反应开始后,甲容器中气体总压强增大,而乙容器中气体总压强不变、气体总体积增大,则各气体浓度减小,化学反应速率比甲容器中的慢,达到平衡所需时间比甲容器中的长;乙容器中反应状态可看成是由甲容器中反应达到平衡后又减压得到,减小压强,化学平衡向气体分子数增大的正反应方向移动,因此乙容器中 $ {CH_{4}} $ 的平衡转化率比甲容器中的大,故乙容器中 $ {CH_{4}} $ 的转化率随时间变化的关系如图所示:
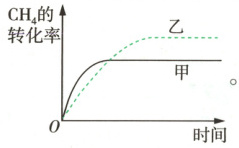
③ 相同温度下,$ {CO_{2}} $ 与 $ {CH_{4}} $ 反应时,$ {CH_{4}} $ 的量相对 $ {CO_{2}} $ 的量越多,即 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $ 越小时,发生反应 (ⅰ) 的程度越大,发生反应 (ⅱ) 的程度越小,导致 $ \dfrac{n({H_{2}})}{n({CO})} $ 越大,故 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $:$ {L_{1}} < {L_{2}} $。反应 (ⅰ)、(ⅱ) 均为吸热反应,升高温度、平衡均正向移动,曲线 $ {L_{2}} $ 中,温度高于 $ 900 \ ^{\circ}C $ 时,$ \dfrac{n({H_{2}})}{n({CO})} $ 减小,说明温度高于 $ 900 \ ^{\circ}C $ 时,可能以反应 (ⅱ) 为主,平衡时 $ {H_{2}} $ 的浓度减小,$ {CO} $ 的浓度增大,导致 $ \dfrac{n({H_{2}})}{n({CO})} $ 减小。
(4) ① 反应 Ⅰ 为反应前后气体分子数减小的放热反应,反应 Ⅱ 为反应前后气体分子数不变的吸热反应,增大压强,反应 Ⅰ 平衡正向移动,反应 Ⅱ 平衡不移动,$ {CO_{2}} $ 的平衡转化率增大,由题图 4 可知,随着 $ Y $ 的增大,$ {CO_{2}} $ 的平衡转化率逐渐减小,故 $ Y $ 表示温度,$ X $ 表示压强。
② 平衡常数 $ K $ 只与温度有关,反应 Ⅰ 为放热反应,温度升高,化学平衡常数 $ K $ 减小,故 $ a $、$ b $、$ c $ 三点对应的反应 Ⅰ 的化学平衡常数 $ K $ 由大到小的顺序为 $ a > b > c $。
③ 由题意可知,$ Y_{1} $ 温度、$ X_{2} $ 压强下,向密闭容器内加入 $ 1 \ mol \ {CO_{2}(g)} $ 和 $ 1 \ mol \ {H_{2}(g)} $,平衡时 $ {CO_{2}} $ 的转化率为 $ 60\% $,设生成的 $ {HCOOH} $ 和 $ {CO} $ 的物质的量分别为 $ x \ mol $、$ y \ mol $,则 $ \dfrac{(x + y) \ mol}{1 \ mol} × 100\% = 60\% $,结合 $ p({HCOOH}) = 5p({CO}) $,则有 $ x = 5y $,解得 $ x = 0.5 $、$ y = 0.1 $,且反应 Ⅰ、Ⅱ 中反应物 $ {CO_{2}} $、$ {H_{2}} $ 的化学计量数相同,则平衡时 $ {CO_{2}} $ 和 $ {H_{2}} $ 的转化率相同,故平衡时两者的物质的量均为 $ 0.4 \ mol $,由反应 Ⅱ 可知,平衡时生成的 $ {H_{2}O} $ 的物质的量等于生成的 $ {CO} $ 的,则平衡时 $ {H_{2}O} $ 的物质的量为 $ 0.1 \ mol $,故气体的总物质的量为 $ 1.5 \ mol $,则反应 Ⅰ 的 $ K_{p} = \dfrac{\dfrac{0.5 \ mol}{1.5 \ mol} × X_{2}}{\left( \dfrac{0.4 \ mol}{1.5 \ mol} × X_{2} \right)^{2}} = \dfrac{75}{16X_{2}} $。
答案
(1) $ \Delta H_{1} + \Delta H_{2} $
(2) $ 0.05 $ $ 50\% $
(3) ① 该反应的 $ \Delta S > 0 $、$ \Delta H > 0 $,故在高温条件下,可使 $ \Delta H - T\Delta S < 0 $,使反应可自发进行
② 见解析
③ $ < $ 温度高于 $ 900 \ ^{\circ}C $ 时,以反应 (ⅱ) 为主,平衡时 $ {H_{2}} $ 的浓度减小,$ {CO} $ 的浓度增大,导致 $ \dfrac{n({H_{2}})}{n({CO})} $ 减小 (或其他合理答案)
(4) ① 温度
② $ a > b > c $
③ $ \dfrac{75}{16X_{2}} $
解析
(1) 结合盖斯定律可知,目标反应 $ = $ 反应ⅰ $ + $ 反应ⅱ,则反应 $ {CO_{2}(g) + 3H_{2}(g){<=>[][]}CH_{3}OH(g) + H_{2}O(g)} $ 的焓变 $ \Delta H = \Delta H_{1} + \Delta H_{2} $。
(2) 设达到平衡时 $ {CO} $ 的转化量为 $ x \ mol $,可列三段式:
$ \begin{array}{cccccc} & {CO(g)} & + & {H_{2}O(g)} & {<=>[][]} & {CO_{2}(g)} & + & {H_{2}(g)} \\ 起始量/mol & 1 & & 1 & & 0 & & 0 \\ 转化量/mol & x & & x & & x & & x \\ 平衡量/mol & 1 - x & & 1 - x & & x & & x \end{array} $
则该反应的平衡常数 $ K = \dfrac{x^{2}}{(1 - x)^{2}} = 1.0 $,解得 $ x = 0.5 $,则平衡时,$ n({CO}) = n({H_{2}O}) = $
【解题突破】对于反应前后气体分子数不变的反应,可直接用物质的量代替物质的量浓度、分压来计算 $ K_{c} $、$ K_{p} $。
$ n({CO_{2}}) = n({H_{2}}) = 0.5 \ mol $;$ {CO(g)} $ 的转化率为 $ \dfrac{0.5 \ mol}{1 \ mol} × 100\% = 50\% $,$ 0~5 \ min $ 内,$ {H_{2}} $ 的平均反应速率为 $ \dfrac{0.5 \ mol}{2 \ L × 5 \ min} = 0.05 \ mol · L^{-1} · min^{-1} $。
(3) ① 反应 (ⅰ) 为反应前后气体分子数增大的反应,$ \Delta S > 0 $,又 $ \Delta H > 0 $,在高温条件下,有 $ \Delta H - T\Delta S < 0 $,此时该反应能够自发进行。
② 根据题图 1 可知,甲容器中反应条件是恒温恒容,乙容器中反应条件是恒温恒压。反应开始时甲、乙两容器初始容积相等,在相同温度下发生反应 (ⅰ)$ {CH_{4}(g) + CO_{2}(g){<=>[][]}2CO(g) + 2H_{2}(g)} $ $ \Delta H = +245.4 \ kJ · mol^{-1} $;反应开始后,甲容器中气体总压强增大,而乙容器中气体总压强不变、气体总体积增大,则各气体浓度减小,化学反应速率比甲容器中的慢,达到平衡所需时间比甲容器中的长;乙容器中反应状态可看成是由甲容器中反应达到平衡后又减压得到,减小压强,化学平衡向气体分子数增大的正反应方向移动,因此乙容器中 $ {CH_{4}} $ 的平衡转化率比甲容器中的大,故乙容器中 $ {CH_{4}} $ 的转化率随时间变化的关系如图所示:

③ 相同温度下,$ {CO_{2}} $ 与 $ {CH_{4}} $ 反应时,$ {CH_{4}} $ 的量相对 $ {CO_{2}} $ 的量越多,即 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $ 越小时,发生反应 (ⅰ) 的程度越大,发生反应 (ⅱ) 的程度越小,导致 $ \dfrac{n({H_{2}})}{n({CO})} $ 越大,故 $ \dfrac{n({CO_{2}})}{n({CH_{4}})} $:$ {L_{1}} < {L_{2}} $。反应 (ⅰ)、(ⅱ) 均为吸热反应,升高温度、平衡均正向移动,曲线 $ {L_{2}} $ 中,温度高于 $ 900 \ ^{\circ}C $ 时,$ \dfrac{n({H_{2}})}{n({CO})} $ 减小,说明温度高于 $ 900 \ ^{\circ}C $ 时,可能以反应 (ⅱ) 为主,平衡时 $ {H_{2}} $ 的浓度减小,$ {CO} $ 的浓度增大,导致 $ \dfrac{n({H_{2}})}{n({CO})} $ 减小。
(4) ① 反应 Ⅰ 为反应前后气体分子数减小的放热反应,反应 Ⅱ 为反应前后气体分子数不变的吸热反应,增大压强,反应 Ⅰ 平衡正向移动,反应 Ⅱ 平衡不移动,$ {CO_{2}} $ 的平衡转化率增大,由题图 4 可知,随着 $ Y $ 的增大,$ {CO_{2}} $ 的平衡转化率逐渐减小,故 $ Y $ 表示温度,$ X $ 表示压强。
② 平衡常数 $ K $ 只与温度有关,反应 Ⅰ 为放热反应,温度升高,化学平衡常数 $ K $ 减小,故 $ a $、$ b $、$ c $ 三点对应的反应 Ⅰ 的化学平衡常数 $ K $ 由大到小的顺序为 $ a > b > c $。
③ 由题意可知,$ Y_{1} $ 温度、$ X_{2} $ 压强下,向密闭容器内加入 $ 1 \ mol \ {CO_{2}(g)} $ 和 $ 1 \ mol \ {H_{2}(g)} $,平衡时 $ {CO_{2}} $ 的转化率为 $ 60\% $,设生成的 $ {HCOOH} $ 和 $ {CO} $ 的物质的量分别为 $ x \ mol $、$ y \ mol $,则 $ \dfrac{(x + y) \ mol}{1 \ mol} × 100\% = 60\% $,结合 $ p({HCOOH}) = 5p({CO}) $,则有 $ x = 5y $,解得 $ x = 0.5 $、$ y = 0.1 $,且反应 Ⅰ、Ⅱ 中反应物 $ {CO_{2}} $、$ {H_{2}} $ 的化学计量数相同,则平衡时 $ {CO_{2}} $ 和 $ {H_{2}} $ 的转化率相同,故平衡时两者的物质的量均为 $ 0.4 \ mol $,由反应 Ⅱ 可知,平衡时生成的 $ {H_{2}O} $ 的物质的量等于生成的 $ {CO} $ 的,则平衡时 $ {H_{2}O} $ 的物质的量为 $ 0.1 \ mol $,故气体的总物质的量为 $ 1.5 \ mol $,则反应 Ⅰ 的 $ K_{p} = \dfrac{\dfrac{0.5 \ mol}{1.5 \ mol} × X_{2}}{\left( \dfrac{0.4 \ mol}{1.5 \ mol} × X_{2} \right)^{2}} = \dfrac{75}{16X_{2}} $。
答案
(1) $ \Delta H_{1} + \Delta H_{2} $
(2) $ 0.05 $ $ 50\% $
(3) ① 该反应的 $ \Delta S > 0 $、$ \Delta H > 0 $,故在高温条件下,可使 $ \Delta H - T\Delta S < 0 $,使反应可自发进行
② 见解析
③ $ < $ 温度高于 $ 900 \ ^{\circ}C $ 时,以反应 (ⅱ) 为主,平衡时 $ {H_{2}} $ 的浓度减小,$ {CO} $ 的浓度增大,导致 $ \dfrac{n({H_{2}})}{n({CO})} $ 减小 (或其他合理答案)
(4) ① 温度
② $ a > b > c $
③ $ \dfrac{75}{16X_{2}} $
查看更多完整答案,请扫码查看


