2025年天星教育试题调研化学第9辑
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天星教育试题调研化学第9辑 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
原创预测 为了实现碳达峰和碳中和的目标,将 CO₂转化成可利用的化学能源的“负碳”技术是世界各国关注的焦点。
方法Ⅰ:CO₂催化加氢制甲醇。
以 CO₂、H₂为原料合成 CH₃OH 涉及的反应如下:
反应Ⅰ:CO₂(g) + 3H₂(g)⇌CH₃OH(g) + H₂O(g) ΔH₁ = -49.0 kJ·mol⁻¹;
反应Ⅱ:CO₂(g) + H₂(g)⇌CO(g) + H₂O(g) ΔH₂ = +41.0 kJ·mol⁻¹;
反应Ⅲ:CO(g) + 2H₂(g)⇌CH₃OH(g) ΔH₃。
(1)①反应Ⅲ的 ΔH₃ =
②现利用反应Ⅰ和反应Ⅲ两个反应合成 CH₃OH,已知 CO 可使反应的催化剂的寿命降低。若氢碳比表示为 x = $\frac{n(H₂) - n(CO₂)}{n(CO) + n(CO₂)}$,则理论上 x =
(2)250℃,在甲(容积为 4 L)、乙(容积为 2 L)两刚性容器中分别充入 2 mol CO₂和 6 mol H₂,在适宜的催化剂作用下发生反应Ⅰ,容器内总压强随时间变化如图 1 所示。
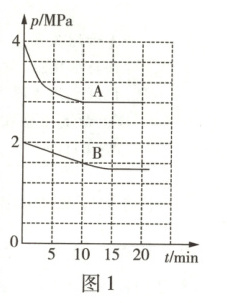
①其中曲线 B 对应
②利用图中数据计算 250℃时,反应Ⅰ的压强平衡常数 $K_p$ =
方法Ⅱ:CO₂催化加氢制甲酸。
(3)已知 CO₂(g) + H₂(g)⇌HCOOH(g) ΔH = -31.4 kJ·mol⁻¹。T₁℃下达到平衡时,化学平衡常数 K = 1.8。实验测得 $v_{正}$ = $k_{正}$c(CO₂)·c(H₂)、$v_{逆}$ = $k_{逆}$c(HCOOH),$k_{正}$、$k_{逆}$为速率常数。T₁℃下,$k_{正}$ =
方法Ⅲ:CO₂催化还原为烃。
(4)光催化 CO₂可制备甲烷,同时实现 O₂的再生,其原理如图 2 所示。
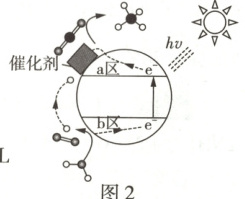
①a 区的电极反应式为
②该装置若生成 1 mol O₂,则理论上消耗 CO₂的体积为
命题依据
化学反应原理综合题是高考化学重要题型,常以社会热点、工业生产等为情境载体,以图像、表格等形式进行命题,考查反应热、平衡常数相关计算等。本题融合反应历程、电化学等进行创新考查,综合性强,难度较大,侧重考查考生提取信息、分析问题、解决问题的能力,符合当前高考化学命题趋势。
方法Ⅰ:CO₂催化加氢制甲醇。
以 CO₂、H₂为原料合成 CH₃OH 涉及的反应如下:
反应Ⅰ:CO₂(g) + 3H₂(g)⇌CH₃OH(g) + H₂O(g) ΔH₁ = -49.0 kJ·mol⁻¹;
反应Ⅱ:CO₂(g) + H₂(g)⇌CO(g) + H₂O(g) ΔH₂ = +41.0 kJ·mol⁻¹;
反应Ⅲ:CO(g) + 2H₂(g)⇌CH₃OH(g) ΔH₃。
(1)①反应Ⅲ的 ΔH₃ =
-90.0
kJ·mol⁻¹。②现利用反应Ⅰ和反应Ⅲ两个反应合成 CH₃OH,已知 CO 可使反应的催化剂的寿命降低。若氢碳比表示为 x = $\frac{n(H₂) - n(CO₂)}{n(CO) + n(CO₂)}$,则理论上 x =
2
时,原料气的利用率最高。但生产中往往采用略高于该值的氢碳比,理由是 减缓反应的催化剂寿命的降低
。(2)250℃,在甲(容积为 4 L)、乙(容积为 2 L)两刚性容器中分别充入 2 mol CO₂和 6 mol H₂,在适宜的催化剂作用下发生反应Ⅰ,容器内总压强随时间变化如图 1 所示。

①其中曲线 B 对应
甲
(填“甲”或“乙”)容器中压强的变化情况。②利用图中数据计算 250℃时,反应Ⅰ的压强平衡常数 $K_p$ =
25/48
MPa⁻²(结果用分数表示)。方法Ⅱ:CO₂催化加氢制甲酸。
(3)已知 CO₂(g) + H₂(g)⇌HCOOH(g) ΔH = -31.4 kJ·mol⁻¹。T₁℃下达到平衡时,化学平衡常数 K = 1.8。实验测得 $v_{正}$ = $k_{正}$c(CO₂)·c(H₂)、$v_{逆}$ = $k_{逆}$c(HCOOH),$k_{正}$、$k_{逆}$为速率常数。T₁℃下,$k_{正}$ =
1.8
$k_{逆}$;若 T₂℃下达到平衡时,$k_{正}$ = 1.9$k_{逆}$,则 T₂ <
(填“>”“<”或“=”)T₁。方法Ⅲ:CO₂催化还原为烃。
(4)光催化 CO₂可制备甲烷,同时实现 O₂的再生,其原理如图 2 所示。

①a 区的电极反应式为
CO₂ + 8H⁺ + 8e⁻ ⇌ CH₄ + 2H₂O
。②该装置若生成 1 mol O₂,则理论上消耗 CO₂的体积为
11.2
L(标准状况下)。命题依据
化学反应原理综合题是高考化学重要题型,常以社会热点、工业生产等为情境载体,以图像、表格等形式进行命题,考查反应热、平衡常数相关计算等。本题融合反应历程、电化学等进行创新考查,综合性强,难度较大,侧重考查考生提取信息、分析问题、解决问题的能力,符合当前高考化学命题趋势。
答案:
解析
(1)①根据盖斯定律可知,反应Ⅲ = 反应Ⅰ - 反应Ⅱ,则 ΔH₃ = ΔH₁ - ΔH₂ = -49.0 kJ·mol⁻¹ - (+41.0 kJ·mol⁻¹) = -90.0 kJ·mol⁻¹。②理论上按反应方程式中化学计量数之比投入原料气,原料气的利用率最高,即反应Ⅰ中投料 n₁(H₂) = 3n(CO₂),反应Ⅲ中投料 n₂(H₂) = 2n(CO)时原料气利用率最高,此时 n(H₂) = 2n(CO) + 3n(CO₂),理论上 x = $\frac{n(H₂) - n(CO₂)}{n(CO) + n(CO₂)}$ = $\frac{2n(CO) + 3n(CO₂) - n(CO₂)}{n(CO) + n(CO₂)}$ = 2。已知 CO 可使反应的催化剂的寿命降低,适当增大 H₂的量,可促使 CO 充分反应,减缓催化剂寿命的降低,故生产中往往采用略高于该值的氢碳比。
(2)①由题图 1 可知,曲线 A 的起始压强比曲线 B 的大,甲容器容积为 4 L,乙容器容积为 2 L,温度相同且起始投料量一样,则容积小的容器内压强大,可推出曲线 A、B 分别对应乙、甲容器中压强的变化情况。②由曲线 A 可知容器内起始压强为 4 MPa,平衡时压强为 2.8 MPa,设反应Ⅰ达到平衡时 CO₂的转化量为 x mol,则列三段式:
| | CO₂(g) + 3H₂(g)⇌CH₃OH(g) + H₂O(g) | | | |
| --- | --- | --- | --- | --- |
| 起始量/mol | 2 | 6 | 0 | 0 |
| 转化量/mol | x | 3x | x | x |
| 平衡量/mol | 2 - x | 6 - 3x | x | x |
平衡时混合气体的总物质的量为(8 - 2x) mol,根据恒温恒容下,气体物质的量之比等于其压强之比可知,$\frac{4 MPa}{2.8 MPa}$ = $\frac{8 mol}{(8 - 2x) mol}$,解得 x = 1.2,则平衡时 CO₂、H₂、CH₃OH、H₂O 的物质的量分别为 0.8 mol、2.4 mol、1.2 mol、1.2 mol,则反应Ⅰ的压强平衡常数 $K_p$ = $\frac{p(H₂O)·p(CH₃OH)}{p³(H₂)·p(CO₂)}$ = $\frac{(\frac{1.2 mol}{5.6 mol}×2.8 MPa)²}{(\frac{2.4 mol}{5.6 mol}×2.8 MPa)³×\frac{0.8 mol}{5.6 mol}×2.8 MPa}$ = $\frac{25}{48}$ MPa⁻²。
(3)平衡时 $v_{正}$ = $v_{逆}$,即 $k_{正}$c(CO₂)·c(H₂) = $k_{逆}$c(HCOOH),则 T₁℃下,K = $\frac{c(HCOOH)}{c(CO₂)·c(H₂)}$ = $\frac{k_{正}}{k_{逆}}$ = 1.8,即 $k_{正}$ = 1.8$k_{逆}$;T₂℃下,$k_{正}$ = 1.9$k_{逆}$,则该温度下 K = 1.9,即 T₁℃→T₂℃,平衡常数 K 增大,平衡正向移动,已知该反应为放热反应,则 T₂ < T₁。
(4)①由题图 2 可知,a 区发生得电子的还原反应 CO₂ + 8H⁺ + 8e⁻ ⇌ CH₄ + 2H₂O,b 区发生失电子的氧化反应 2H₂O - 4e⁻ ⇌ O₂↑ + 4H⁺。②由上述分析可知,每生成 1 mol O₂,电路中转移 4 mol 电子,则理论上消耗 0.5 mol CO₂,标准状况下的体积为 11.2 L。
答案
(1)① -90.0 ② 2 减缓反应的催化剂寿命的降低
(2)①甲 ② $\frac{25}{48}$
(3)1.8 <
(4)① CO₂ + 8H⁺ + 8e⁻ ⇌ CH₄ + 2H₂O ② 11.2
(1)①根据盖斯定律可知,反应Ⅲ = 反应Ⅰ - 反应Ⅱ,则 ΔH₃ = ΔH₁ - ΔH₂ = -49.0 kJ·mol⁻¹ - (+41.0 kJ·mol⁻¹) = -90.0 kJ·mol⁻¹。②理论上按反应方程式中化学计量数之比投入原料气,原料气的利用率最高,即反应Ⅰ中投料 n₁(H₂) = 3n(CO₂),反应Ⅲ中投料 n₂(H₂) = 2n(CO)时原料气利用率最高,此时 n(H₂) = 2n(CO) + 3n(CO₂),理论上 x = $\frac{n(H₂) - n(CO₂)}{n(CO) + n(CO₂)}$ = $\frac{2n(CO) + 3n(CO₂) - n(CO₂)}{n(CO) + n(CO₂)}$ = 2。已知 CO 可使反应的催化剂的寿命降低,适当增大 H₂的量,可促使 CO 充分反应,减缓催化剂寿命的降低,故生产中往往采用略高于该值的氢碳比。
(2)①由题图 1 可知,曲线 A 的起始压强比曲线 B 的大,甲容器容积为 4 L,乙容器容积为 2 L,温度相同且起始投料量一样,则容积小的容器内压强大,可推出曲线 A、B 分别对应乙、甲容器中压强的变化情况。②由曲线 A 可知容器内起始压强为 4 MPa,平衡时压强为 2.8 MPa,设反应Ⅰ达到平衡时 CO₂的转化量为 x mol,则列三段式:
| | CO₂(g) + 3H₂(g)⇌CH₃OH(g) + H₂O(g) | | | |
| --- | --- | --- | --- | --- |
| 起始量/mol | 2 | 6 | 0 | 0 |
| 转化量/mol | x | 3x | x | x |
| 平衡量/mol | 2 - x | 6 - 3x | x | x |
平衡时混合气体的总物质的量为(8 - 2x) mol,根据恒温恒容下,气体物质的量之比等于其压强之比可知,$\frac{4 MPa}{2.8 MPa}$ = $\frac{8 mol}{(8 - 2x) mol}$,解得 x = 1.2,则平衡时 CO₂、H₂、CH₃OH、H₂O 的物质的量分别为 0.8 mol、2.4 mol、1.2 mol、1.2 mol,则反应Ⅰ的压强平衡常数 $K_p$ = $\frac{p(H₂O)·p(CH₃OH)}{p³(H₂)·p(CO₂)}$ = $\frac{(\frac{1.2 mol}{5.6 mol}×2.8 MPa)²}{(\frac{2.4 mol}{5.6 mol}×2.8 MPa)³×\frac{0.8 mol}{5.6 mol}×2.8 MPa}$ = $\frac{25}{48}$ MPa⁻²。
(3)平衡时 $v_{正}$ = $v_{逆}$,即 $k_{正}$c(CO₂)·c(H₂) = $k_{逆}$c(HCOOH),则 T₁℃下,K = $\frac{c(HCOOH)}{c(CO₂)·c(H₂)}$ = $\frac{k_{正}}{k_{逆}}$ = 1.8,即 $k_{正}$ = 1.8$k_{逆}$;T₂℃下,$k_{正}$ = 1.9$k_{逆}$,则该温度下 K = 1.9,即 T₁℃→T₂℃,平衡常数 K 增大,平衡正向移动,已知该反应为放热反应,则 T₂ < T₁。
(4)①由题图 2 可知,a 区发生得电子的还原反应 CO₂ + 8H⁺ + 8e⁻ ⇌ CH₄ + 2H₂O,b 区发生失电子的氧化反应 2H₂O - 4e⁻ ⇌ O₂↑ + 4H⁺。②由上述分析可知,每生成 1 mol O₂,电路中转移 4 mol 电子,则理论上消耗 0.5 mol CO₂,标准状况下的体积为 11.2 L。
答案
(1)① -90.0 ② 2 减缓反应的催化剂寿命的降低
(2)①甲 ② $\frac{25}{48}$
(3)1.8 <
(4)① CO₂ + 8H⁺ + 8e⁻ ⇌ CH₄ + 2H₂O ② 11.2
查看更多完整答案,请扫码查看


