2025年天星教育试题调研化学第9辑
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年天星教育试题调研化学第9辑 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
原创预测2 小分子在科学研究和生产实践中有着重要作用。$CO_{2}$和$NH_{3}$均为小分子,具有广泛用途。请回答下列问题:
Ⅰ.$CO_{2}$在化工合成中的应用。
ⅰ. 甲醇的制备:利用$CO_{2}$和$H_{2}$合成甲醇,主要涉及以下反应。
反应①:$CO_{2}(g)+3H_{2}(g)\rightleftharpoons CH_{3}OH(g)+H_{2}O(g)$ $\Delta H_{1}=-49kJ· mol^{-1}$;
反应②:$CO_{2}(g)+H_{2}\rightleftharpoons CO(g)+H_{2}O(g)$ $\Delta H_{2}=+41kJ· mol^{-1}$。
在$1L$的密闭容器中,加入催化剂,并投入$1molCO_{2}$和$3molH_{2}$发生上述两个反应,平衡时,$CO_{2}$的转化率和甲醇的选择性随温度的变化趋势如图1所示。
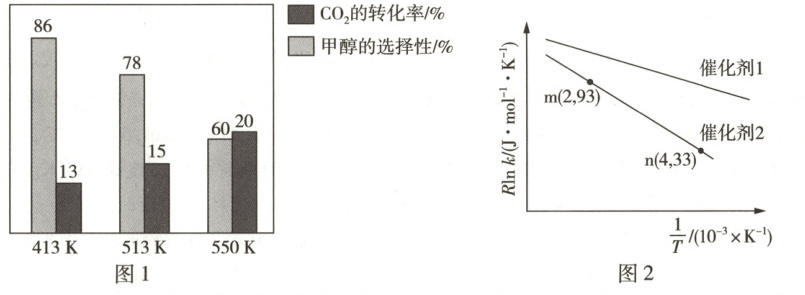
(1)由图1可知,制备甲醇最适宜的温度为
(2)$550K$下,达到平衡时,若该反应体系的总压强为$p$,则反应①的$K_{p}=$
ⅱ. 甲酸$(HCOOH)$的制备:工业上制备甲酸的原理为$CO_{2}(g)+H_{2}(g)\rightleftharpoons HCOOH(g)$,该反应的速率方程为$v = k· c(CO_{2})· c(H_{2})$。
(3)已知Arrhenius经验公式为$R\ln k=-\frac{E_{a}}{T}+C$($E_{a}$为活化能,$k$为速率常数,$R$和$C$均为常数)。在催化剂1和催化剂2作用下,测得反应$CO_{2}(g)+H_{2}(g)\rightleftharpoons HCOOH(g)$的$R\ln k$与$\frac{1}{T}$的关系如图2所示。其中催化效率比较高的是
Ⅱ.$NH_{3}$在生活、科研等方面的应用。
ⅲ. 利用$NH_{3}$消除$NO$污染:$NO$是主要大气污染物,利用$NH_{3}$消除$NO$的原理为$4NH_{3}(g)+6NO(g)\rightleftharpoons 5N_{2}(g)+6H_{2}O(g)$ $\Delta H\lt0$。
(4)①该反应在
②向某恒容绝热的密闭容器中加入等物质的量的$NH_{3}(g)$和$NO(g)$发生上述反应,下列叙述能说明反应已经达到平衡状态的是
A. $v(NO)=v(H_{2}O)$
B. 相同时间内断裂$N—H$键、$H—O$键的数目相同
C. 化学平衡常数不再变化
D. 混合气体的平均相对分子质量不再变化
ⅳ.$NH_{3}$在配合物领域中的应用:溶液中$NH_{3}$能与多种金属阳离子形成配合物,配合物稳定常数$K_{f}$可以用来描述配体与配离子之间相互作用的强度,其定义如下($M$代表中心金属原子或金属离子,$L$代表配体,$n$代表配体数量):$M + nL\rightleftharpoons ML_{n}$ $K_{f}(ML_{n})=\frac{c(ML_{n})}{c(M)· c^{n}(L)}$。
(5)已知:常温下,$K_{sp}(AgCl)=1.8×10^{-10}$,$K_{f}\{[Ag(NH_{3})_{2}]^{+}\}=2.5×10^{7}$,忽略$NH_{3}· H_{2}O$的电离,若使$0.05molAgCl$完全溶解于$1L$氨水中,则氨水的浓度$c(NH_{3}· H_{2}O)$至少为
Ⅰ.$CO_{2}$在化工合成中的应用。
ⅰ. 甲醇的制备:利用$CO_{2}$和$H_{2}$合成甲醇,主要涉及以下反应。
反应①:$CO_{2}(g)+3H_{2}(g)\rightleftharpoons CH_{3}OH(g)+H_{2}O(g)$ $\Delta H_{1}=-49kJ· mol^{-1}$;
反应②:$CO_{2}(g)+H_{2}\rightleftharpoons CO(g)+H_{2}O(g)$ $\Delta H_{2}=+41kJ· mol^{-1}$。
在$1L$的密闭容器中,加入催化剂,并投入$1molCO_{2}$和$3molH_{2}$发生上述两个反应,平衡时,$CO_{2}$的转化率和甲醇的选择性随温度的变化趋势如图1所示。

(1)由图1可知,制备甲醇最适宜的温度为
513K
(填“$413K$”“$513K$”或“$550K$”)。(2)$550K$下,达到平衡时,若该反应体系的总压强为$p$,则反应①的$K_{p}=$
$\frac{\frac{0.12}{3.76}p×\frac{0.2}{3.76}p}{\frac{0.8}{3.76}p×(\frac{2.56}{3.76}p)^{3}}$
(列出计算式即可)。ⅱ. 甲酸$(HCOOH)$的制备:工业上制备甲酸的原理为$CO_{2}(g)+H_{2}(g)\rightleftharpoons HCOOH(g)$,该反应的速率方程为$v = k· c(CO_{2})· c(H_{2})$。
(3)已知Arrhenius经验公式为$R\ln k=-\frac{E_{a}}{T}+C$($E_{a}$为活化能,$k$为速率常数,$R$和$C$均为常数)。在催化剂1和催化剂2作用下,测得反应$CO_{2}(g)+H_{2}(g)\rightleftharpoons HCOOH(g)$的$R\ln k$与$\frac{1}{T}$的关系如图2所示。其中催化效率比较高的是
催化剂1
(填“催化剂1”或“催化剂2”),在催化剂2的作用下,活化能$E_{a}=$30
$kJ· mol^{-1}$。Ⅱ.$NH_{3}$在生活、科研等方面的应用。
ⅲ. 利用$NH_{3}$消除$NO$污染:$NO$是主要大气污染物,利用$NH_{3}$消除$NO$的原理为$4NH_{3}(g)+6NO(g)\rightleftharpoons 5N_{2}(g)+6H_{2}O(g)$ $\Delta H\lt0$。
(4)①该反应在
任意条件
(填“高温”“低温”或“任意条件”)下能自发进行。②向某恒容绝热的密闭容器中加入等物质的量的$NH_{3}(g)$和$NO(g)$发生上述反应,下列叙述能说明反应已经达到平衡状态的是
BCD
(填标号)。A. $v(NO)=v(H_{2}O)$
B. 相同时间内断裂$N—H$键、$H—O$键的数目相同
C. 化学平衡常数不再变化
D. 混合气体的平均相对分子质量不再变化
ⅳ.$NH_{3}$在配合物领域中的应用:溶液中$NH_{3}$能与多种金属阳离子形成配合物,配合物稳定常数$K_{f}$可以用来描述配体与配离子之间相互作用的强度,其定义如下($M$代表中心金属原子或金属离子,$L$代表配体,$n$代表配体数量):$M + nL\rightleftharpoons ML_{n}$ $K_{f}(ML_{n})=\frac{c(ML_{n})}{c(M)· c^{n}(L)}$。
(5)已知:常温下,$K_{sp}(AgCl)=1.8×10^{-10}$,$K_{f}\{[Ag(NH_{3})_{2}]^{+}\}=2.5×10^{7}$,忽略$NH_{3}· H_{2}O$的电离,若使$0.05molAgCl$完全溶解于$1L$氨水中,则氨水的浓度$c(NH_{3}· H_{2}O)$至少为
$\frac{\sqrt{5}}{3}+0.1$
$mol· L^{-1}$(列出计算式即可)。
答案:
解析
(1)由题意可知,首先应选择达到平衡时甲醇的选择性比较高的温度,则排除$550K$,$413K$和$513K$下达到平衡时甲醇的选择性和$CO_{2}$的转化率都相差不大,计算产率可知$413K$下,平衡时$n(CH_{3}OH)=1mol×86\%×13\%=0.1118mol$,$513K$下,平衡时$n(CH_{3}OH)=1mol×78\%×15\%=0.1170mol$,故制备甲醇最适宜的温度为$513K$。
(2)第一步,结合图像信息,计算消耗的$CO_{2}$的物质的量及生成$CO$消耗的$CO_{2}$的物质的量。根据题图1可知,$550K$下,平衡时,$CO_{2}$的转化率为$20\%$,则消耗的$CO_{2}$的物质的量为$1mol×20\%=0.2mol$,平衡时$CO_{2}$的物质的量为$1mol - 0.2mol = 0.8mol$;甲醇的选择性为$60\%$,则生成甲醇消耗的$CO_{2}$的物质的量为$0.2mol×60\%=0.12mol$,故生成$CO$消耗的$CO_{2}$的物质的量为$0.2mol - 0.12mol = 0.08mol$。第二步,列三段式,计算各物质的分压。根据上述数据可列三段式:
$CO_{2}(g)+3H_{2}(g)\rightleftharpoons CH_{3}OH(g)+H_{2}O(g)$
|起始量/mol|1|3|0|0|
|----|----|----|----|----|
|转化量/mol|0.12|0.36|0.12|0.12|
|平衡量/mol|0.8|2.56|0.12|0.2|
$CO_{2}(g)+H_{2}(g)\rightleftharpoons CO(g)+H_{2}O(g)$
|起始量/mol|1|3|0|0|
|----|----|----|----|----|
|转化量/mol|0.08|0.08|0.08|0.08|
|平衡量/mol|0.8|2.56|0.08|0.2|
达到平衡时,体系中各物质的物质的量分别为$n(CO_{2}) = 0.8mol$,$n(H_{2}) = 2.56mol$,$n(CH_{3}OH) = 0.12mol$,$n(CO) = 0.08mol$,$n(H_{2}O) = 0.2mol$,则平衡时混合气体的总物质的量为$(0.8 + 2.56 + 0.12 + 0.08 + 0.2)mol = 3.76mol$。已知$550K$下,平衡时该反应体系的总压强为$p$,则$p(CO_{2})=\frac{0.8}{3.76}p$,$p(CH_{3}OH)=\frac{0.12}{3.76}p$,$p(H_{2})=\frac{2.56}{3.76}p$,$p(H_{2}O)=\frac{0.2}{3.76}p$,反应①的$K_{p}=\frac{p(CH_{3}OH)· p(H_{2}O)}{p(CO_{2})· p^{3}(H_{2})}=\frac{\frac{0.12}{3.76}p×\frac{0.2}{3.76}p}{\frac{0.8}{3.76}p×(\frac{2.56}{3.76}p)^{3}}$。
(3)根据Arrhenius经验公式并结合题图2可知,直线斜率的绝对值即为活化能,因此直线斜率的绝对值越小表示活化能越小,而活化能越小说明催化剂的催化效率更高,所以催化效率比较高的是催化剂1。将m、n两点的数据代入Arrhenius经验公式可得$93J· mol^{-1}· K^{-1}=-E_{a}×2×10^{-3}K^{-1}+C$,$33J· mol^{-1}· K^{-1}=-E_{a}×4×10^{-3}K^{-1}+C$,将两式联立可得活化能$E_{a}=30kJ· mol^{-1}$。
(4)①该反应为反应前后气体分子数增大的放热反应,$\Delta H\lt0$、$\Delta S\gt0$,故$\Delta G=\Delta H - T\Delta S\lt0$,该反应在任意条件下都能自发进行。②当$v(NO)=v(H_{2}O)$时,没有指明反应方向,无法说明正逆反应速率是否相等,即不能判断该反应是否达到平衡状态,A不符合题意。根据反应方程式可知,若相同时间内断裂$N—H$键、$H—O$键的数目相同,说明$v_{正}=v_{逆}$,可说明该反应已达到平衡状态,B符合题意。化学平衡常数仅与温度有关,温度不变,平衡常数不变,该反应为放热反应,所以绝热容器中平衡常数不变,即温度不变,可说明该反应已达到平衡状态,C符合题意。根据反应方程式可知,反应未平衡时,混合气体的总质量不变,总物质的量发生变化,即混合气体的平均相对分子质量发生变化,所以当混合气体的平均相对分子质量不再变化时,说明该反应已达到平衡状态,D符合题意。
(5)$AgCl$溶于氨水的离子方程式为$AgCl(s)+2NH_{3}(aq)\rightleftharpoons [Ag(NH_{3})_{2}]^{+}(aq)+Cl^{-}(aq)$,该反应的平衡常数$K=\frac{c\{[Ag(NH_{3})_{2}]^{+}\}· c(Cl^{-})}{c^{2}(NH_{3})}=K_{sp}(AgCl)· K_{f}\{[Ag(NH_{3})_{2}]^{+}\}=1.8×10^{-10}×2.5×10^{7}=4.5×10^{-3}$,假设$0.05molAgCl$已经完全溶解于$1L$、浓度为$c\ mol· L^{-1}$的氨水中,则此时$c\{[Ag(NH_{3})_{2}]^{+}\}=c(Cl^{-})=0.05mol· L^{-1}$,$c(NH_{3}· H_{2}O)=(c - 2×0.05)mol· L^{-1}=(c - 0.1)mol· L^{-1}$,此时的$Q\lt K$,即$Q=\frac{0.05^{2}}{(c - 0.1)^{2}}\lt4.5×10^{-3}$,解得$c\gt\frac{\sqrt{5}}{3}+0.1$。
答案
(1)$513K$
(2)$\frac{\frac{0.12}{3.76}p×\frac{0.2}{3.76}p}{\frac{0.8}{3.76}p×(\frac{2.56}{3.76}p)^{3}}$
(3)催化剂1 $30$
(4)①任意条件 ②BCD
(5)$\frac{\sqrt{5}}{3}+0.1$
(1)由题意可知,首先应选择达到平衡时甲醇的选择性比较高的温度,则排除$550K$,$413K$和$513K$下达到平衡时甲醇的选择性和$CO_{2}$的转化率都相差不大,计算产率可知$413K$下,平衡时$n(CH_{3}OH)=1mol×86\%×13\%=0.1118mol$,$513K$下,平衡时$n(CH_{3}OH)=1mol×78\%×15\%=0.1170mol$,故制备甲醇最适宜的温度为$513K$。
(2)第一步,结合图像信息,计算消耗的$CO_{2}$的物质的量及生成$CO$消耗的$CO_{2}$的物质的量。根据题图1可知,$550K$下,平衡时,$CO_{2}$的转化率为$20\%$,则消耗的$CO_{2}$的物质的量为$1mol×20\%=0.2mol$,平衡时$CO_{2}$的物质的量为$1mol - 0.2mol = 0.8mol$;甲醇的选择性为$60\%$,则生成甲醇消耗的$CO_{2}$的物质的量为$0.2mol×60\%=0.12mol$,故生成$CO$消耗的$CO_{2}$的物质的量为$0.2mol - 0.12mol = 0.08mol$。第二步,列三段式,计算各物质的分压。根据上述数据可列三段式:
$CO_{2}(g)+3H_{2}(g)\rightleftharpoons CH_{3}OH(g)+H_{2}O(g)$
|起始量/mol|1|3|0|0|
|----|----|----|----|----|
|转化量/mol|0.12|0.36|0.12|0.12|
|平衡量/mol|0.8|2.56|0.12|0.2|
$CO_{2}(g)+H_{2}(g)\rightleftharpoons CO(g)+H_{2}O(g)$
|起始量/mol|1|3|0|0|
|----|----|----|----|----|
|转化量/mol|0.08|0.08|0.08|0.08|
|平衡量/mol|0.8|2.56|0.08|0.2|
达到平衡时,体系中各物质的物质的量分别为$n(CO_{2}) = 0.8mol$,$n(H_{2}) = 2.56mol$,$n(CH_{3}OH) = 0.12mol$,$n(CO) = 0.08mol$,$n(H_{2}O) = 0.2mol$,则平衡时混合气体的总物质的量为$(0.8 + 2.56 + 0.12 + 0.08 + 0.2)mol = 3.76mol$。已知$550K$下,平衡时该反应体系的总压强为$p$,则$p(CO_{2})=\frac{0.8}{3.76}p$,$p(CH_{3}OH)=\frac{0.12}{3.76}p$,$p(H_{2})=\frac{2.56}{3.76}p$,$p(H_{2}O)=\frac{0.2}{3.76}p$,反应①的$K_{p}=\frac{p(CH_{3}OH)· p(H_{2}O)}{p(CO_{2})· p^{3}(H_{2})}=\frac{\frac{0.12}{3.76}p×\frac{0.2}{3.76}p}{\frac{0.8}{3.76}p×(\frac{2.56}{3.76}p)^{3}}$。
(3)根据Arrhenius经验公式并结合题图2可知,直线斜率的绝对值即为活化能,因此直线斜率的绝对值越小表示活化能越小,而活化能越小说明催化剂的催化效率更高,所以催化效率比较高的是催化剂1。将m、n两点的数据代入Arrhenius经验公式可得$93J· mol^{-1}· K^{-1}=-E_{a}×2×10^{-3}K^{-1}+C$,$33J· mol^{-1}· K^{-1}=-E_{a}×4×10^{-3}K^{-1}+C$,将两式联立可得活化能$E_{a}=30kJ· mol^{-1}$。
(4)①该反应为反应前后气体分子数增大的放热反应,$\Delta H\lt0$、$\Delta S\gt0$,故$\Delta G=\Delta H - T\Delta S\lt0$,该反应在任意条件下都能自发进行。②当$v(NO)=v(H_{2}O)$时,没有指明反应方向,无法说明正逆反应速率是否相等,即不能判断该反应是否达到平衡状态,A不符合题意。根据反应方程式可知,若相同时间内断裂$N—H$键、$H—O$键的数目相同,说明$v_{正}=v_{逆}$,可说明该反应已达到平衡状态,B符合题意。化学平衡常数仅与温度有关,温度不变,平衡常数不变,该反应为放热反应,所以绝热容器中平衡常数不变,即温度不变,可说明该反应已达到平衡状态,C符合题意。根据反应方程式可知,反应未平衡时,混合气体的总质量不变,总物质的量发生变化,即混合气体的平均相对分子质量发生变化,所以当混合气体的平均相对分子质量不再变化时,说明该反应已达到平衡状态,D符合题意。
(5)$AgCl$溶于氨水的离子方程式为$AgCl(s)+2NH_{3}(aq)\rightleftharpoons [Ag(NH_{3})_{2}]^{+}(aq)+Cl^{-}(aq)$,该反应的平衡常数$K=\frac{c\{[Ag(NH_{3})_{2}]^{+}\}· c(Cl^{-})}{c^{2}(NH_{3})}=K_{sp}(AgCl)· K_{f}\{[Ag(NH_{3})_{2}]^{+}\}=1.8×10^{-10}×2.5×10^{7}=4.5×10^{-3}$,假设$0.05molAgCl$已经完全溶解于$1L$、浓度为$c\ mol· L^{-1}$的氨水中,则此时$c\{[Ag(NH_{3})_{2}]^{+}\}=c(Cl^{-})=0.05mol· L^{-1}$,$c(NH_{3}· H_{2}O)=(c - 2×0.05)mol· L^{-1}=(c - 0.1)mol· L^{-1}$,此时的$Q\lt K$,即$Q=\frac{0.05^{2}}{(c - 0.1)^{2}}\lt4.5×10^{-3}$,解得$c\gt\frac{\sqrt{5}}{3}+0.1$。
答案
(1)$513K$
(2)$\frac{\frac{0.12}{3.76}p×\frac{0.2}{3.76}p}{\frac{0.8}{3.76}p×(\frac{2.56}{3.76}p)^{3}}$
(3)催化剂1 $30$
(4)①任意条件 ②BCD
(5)$\frac{\sqrt{5}}{3}+0.1$
查看更多完整答案,请扫码查看


