2025年自主学习能力测评单元测试八年级数学上册人教版A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年自主学习能力测评单元测试八年级数学上册人教版A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
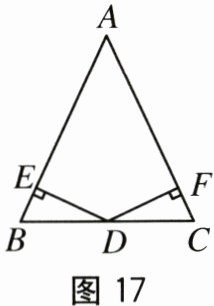
21. (10分)如图17,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证△BDE≌△CDF.
(2)若∠A=60°,BE=1,求AC的长.
(1)求证△BDE≌△CDF.
(2)若∠A=60°,BE=1,求AC的长.

答案:
21.
(1)
∵DE⊥AB,DF⊥AC,
∴∠BED = ∠CFD = 90°。又
∵AB = AC,
∴∠B = ∠C。又
∵D为BC边的中点,
∴BD = CD。在△BDE和△CDF中,
$\begin{cases}$
∠BED = ∠CFD, \\
∠B = ∠C, \\
BD = CD,
$\end{cases}$
∴△BDE≌△CDF(AAS)
(2)
∵AB = AC,∠A = 60°,
∴△ABC为等边三角形,
∴∠B = 60°。
∵∠BED = 90°,
∴∠BDE = 30°,
∴BD = 2BE = 2×1 = 2,
∴BC = 2BD = 4,
∴AC = BC = 4
(1)
∵DE⊥AB,DF⊥AC,
∴∠BED = ∠CFD = 90°。又
∵AB = AC,
∴∠B = ∠C。又
∵D为BC边的中点,
∴BD = CD。在△BDE和△CDF中,
$\begin{cases}$
∠BED = ∠CFD, \\
∠B = ∠C, \\
BD = CD,
$\end{cases}$
∴△BDE≌△CDF(AAS)
(2)
∵AB = AC,∠A = 60°,
∴△ABC为等边三角形,
∴∠B = 60°。
∵∠BED = 90°,
∴∠BDE = 30°,
∴BD = 2BE = 2×1 = 2,
∴BC = 2BD = 4,
∴AC = BC = 4
22. (12分)
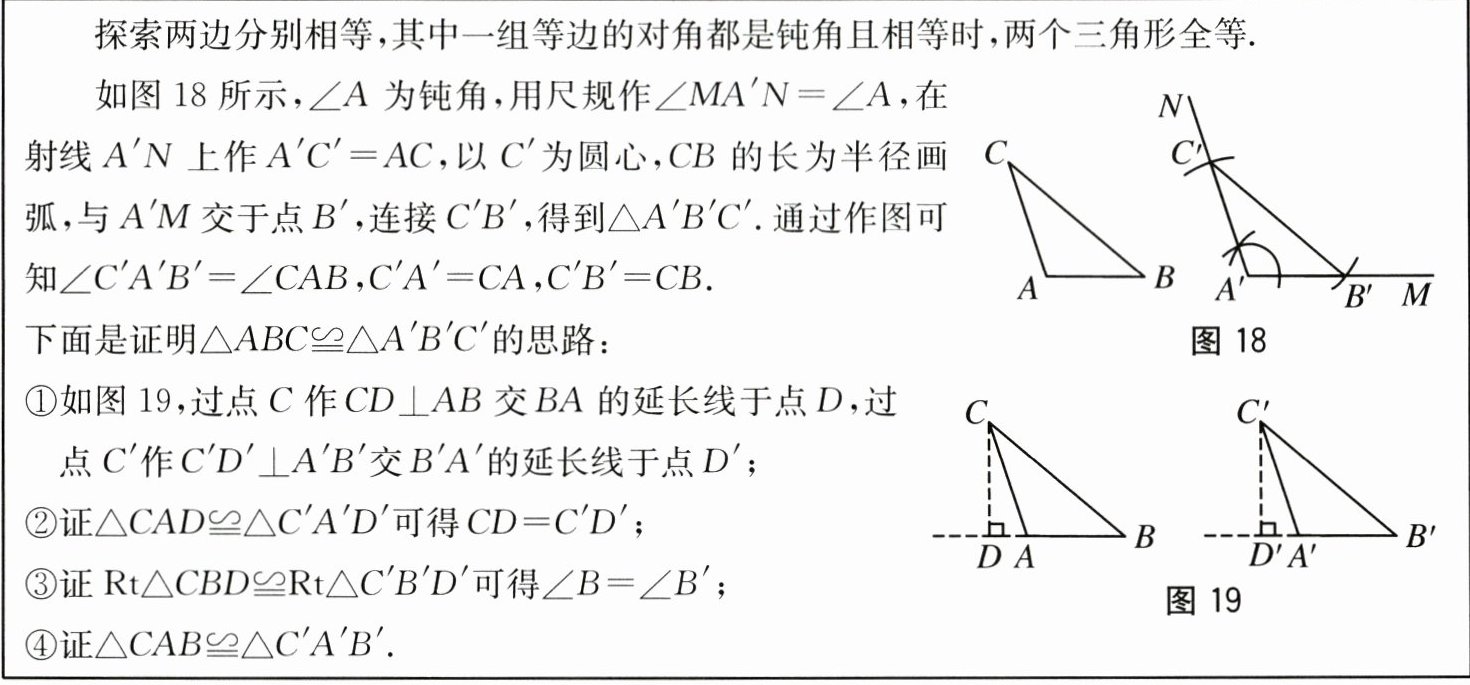
探索两边分别相等,其中一组等边的对角都是钝角且相等时,两个三角形全等.
如图18所示,∠A为钝角,用尺规作∠MA'N=∠A,在射线A'N上作A'C'=AC,以C'为圆心,CB的长为半径画弧,与A'M交于点B',连接C'B',得到△A'B'C'.通过作图可知∠C'A'B'=∠CAB,C'A'=CA,C'B'=CB.
下面是证明△ABC≌△A'B'C'的思路:
①如图19,过点C作CD⊥AB交BA的延长线于点D,过点C'作C'D'⊥A'B'交B'A'的延长线于点D';
②证△CAD≌△C'A'D'可得CD=C'D';
③证Rt△CBD≌Rt△C'B'D'可得∠B=∠B';
④证△CAB≌△C'A'B'.
(1)填空:上述思路②中,证明三角形全等的依据是
(2)补全证明:请你在上述思路①②③的前提下,补充第④部分的证明过程.
(3)判断:
①两边分别相等,其中一组等边的对角都是锐角且相等时,两个三角形全等;
②两边分别相等,其中一组等边的对角都是直角时,两个三角形全等.
上面两种说法,

探索两边分别相等,其中一组等边的对角都是钝角且相等时,两个三角形全等.
如图18所示,∠A为钝角,用尺规作∠MA'N=∠A,在射线A'N上作A'C'=AC,以C'为圆心,CB的长为半径画弧,与A'M交于点B',连接C'B',得到△A'B'C'.通过作图可知∠C'A'B'=∠CAB,C'A'=CA,C'B'=CB.
下面是证明△ABC≌△A'B'C'的思路:
①如图19,过点C作CD⊥AB交BA的延长线于点D,过点C'作C'D'⊥A'B'交B'A'的延长线于点D';
②证△CAD≌△C'A'D'可得CD=C'D';
③证Rt△CBD≌Rt△C'B'D'可得∠B=∠B';
④证△CAB≌△C'A'B'.
(1)填空:上述思路②中,证明三角形全等的依据是
AAS
(填符号简写形式).(2)补全证明:请你在上述思路①②③的前提下,补充第④部分的证明过程.
(3)判断:
①两边分别相等,其中一组等边的对角都是锐角且相等时,两个三角形全等;
②两边分别相等,其中一组等边的对角都是直角时,两个三角形全等.
上面两种说法,
②
说法正确.(直接写序号,不必证明)
答案:
22.
(1)AAS
(2)在△CAB和△C'A'B'中,
$\begin{cases}$
∠CAB = ∠C'A'B', \\
∠B = ∠B', \\
CA = C'A',
$\end{cases}$
∴△CAB≌△C'A'B'(AAS)
(3)② 提示:①两边分别相等,其中一组等边的对角都是锐角且相等时,两个三角形不一定全等;在△ABC和△DEF中,AB = DE,AC = DF,∠B = ∠E < 90°,如答图14,通过作图,可知△ABC与△DEF不一定全等。②两边分别相等,其中一组等边的对角都是直角时,两个三角形全等;在△ABC和△DEF中,AB = DE,AC = DF,∠B = ∠E = 90°,如答图15,Rt△ABC≌Rt△DEF(HL)


22.
(1)AAS
(2)在△CAB和△C'A'B'中,
$\begin{cases}$
∠CAB = ∠C'A'B', \\
∠B = ∠B', \\
CA = C'A',
$\end{cases}$
∴△CAB≌△C'A'B'(AAS)
(3)② 提示:①两边分别相等,其中一组等边的对角都是锐角且相等时,两个三角形不一定全等;在△ABC和△DEF中,AB = DE,AC = DF,∠B = ∠E < 90°,如答图14,通过作图,可知△ABC与△DEF不一定全等。②两边分别相等,其中一组等边的对角都是直角时,两个三角形全等;在△ABC和△DEF中,AB = DE,AC = DF,∠B = ∠E = 90°,如答图15,Rt△ABC≌Rt△DEF(HL)


23. (12分)已知△ABC是等边三角形,点D在边BC上.
【基本图形】(1)如图20,以AD为一边作等边△ADE,连接CE.可得CE+CD=AC,说明理由.
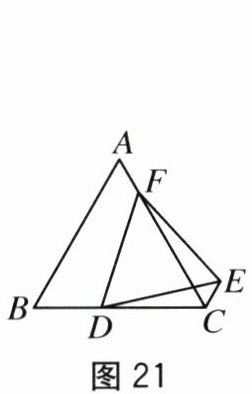
【迁移运用】(2)如图21,点F是AC边上一点,以DF为一边作等边△DEF.求证CE+CD=CF.
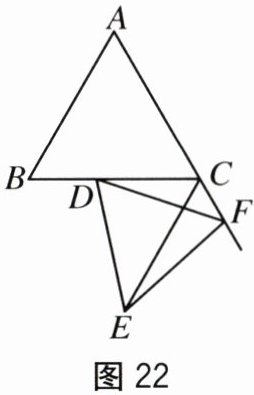
【类比探究】(3)如图22,点F是AC边的延长线上一点,以DF为一边作等边△DEF.直接写出线段CE,CD,CF之间的数量关系,不需证明.
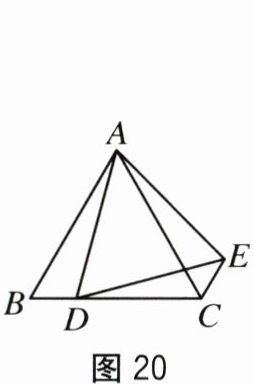
【基本图形】(1)如图20,以AD为一边作等边△ADE,连接CE.可得CE+CD=AC,说明理由.
【迁移运用】(2)如图21,点F是AC边上一点,以DF为一边作等边△DEF.求证CE+CD=CF.
【类比探究】(3)如图22,点F是AC边的延长线上一点,以DF为一边作等边△DEF.直接写出线段CE,CD,CF之间的数量关系,不需证明.



答案:
23.
(1)
∵△ABC与△ADE都是等边三角形,
∴AC = AB = CB,∠CAB = 60°,AD = AE,∠DAE = 60°,
∴∠CAE = ∠DAE - ∠CAD = 60° - ∠CAD,∠BAD = ∠CAB - ∠CAD = 60° - ∠CAD,
∴∠CAE = ∠BAD。在△BAD与△CAE中,
$\begin{cases}$
AB = AC, \\
∠BAD = ∠CAE, \\
AD = AE,
$\end{cases}$
∴△BAD≌△CAE(SAS),
∴BD = CE,
∴CE + CD = BD + CD = CB。
∵AC = CB,
∴CE + CD = AC
(2)过点D作DG//AB,交AC于点G,如答图16。
∵△ABC是等边三角形,
∴∠ACB = ∠A = ∠B = 60°。
∵DG//AB,
∴∠CGD = ∠A = 60°,∠CDG = ∠B = 60°。又
∵∠ACB = 60°,
∴△CDG是等边三角形,
∴CD = DG = CG。
∵△DEF是等边三角形,
∴DE = DF,∠EDF = 60°。
∵∠CDE = ∠CDG - ∠EDG = 60° - ∠EDG,∠GDF = ∠EDF - ∠EDG = 60° - ∠EDG,
∴∠CDE = ∠GDF。在△CDE与△GDF中,
$\begin{cases}$
DC = DG, \\
∠CDE = ∠GDF, \\
DE = DF,
$\end{cases}$
∴△CDE≌△GDF(SAS),
∴CE = GF,
∴CE + CD = GF + CG = CF
(3)CD + CF = CE


23.
(1)
∵△ABC与△ADE都是等边三角形,
∴AC = AB = CB,∠CAB = 60°,AD = AE,∠DAE = 60°,
∴∠CAE = ∠DAE - ∠CAD = 60° - ∠CAD,∠BAD = ∠CAB - ∠CAD = 60° - ∠CAD,
∴∠CAE = ∠BAD。在△BAD与△CAE中,
$\begin{cases}$
AB = AC, \\
∠BAD = ∠CAE, \\
AD = AE,
$\end{cases}$
∴△BAD≌△CAE(SAS),
∴BD = CE,
∴CE + CD = BD + CD = CB。
∵AC = CB,
∴CE + CD = AC
(2)过点D作DG//AB,交AC于点G,如答图16。
∵△ABC是等边三角形,
∴∠ACB = ∠A = ∠B = 60°。
∵DG//AB,
∴∠CGD = ∠A = 60°,∠CDG = ∠B = 60°。又
∵∠ACB = 60°,
∴△CDG是等边三角形,
∴CD = DG = CG。
∵△DEF是等边三角形,
∴DE = DF,∠EDF = 60°。
∵∠CDE = ∠CDG - ∠EDG = 60° - ∠EDG,∠GDF = ∠EDF - ∠EDG = 60° - ∠EDG,
∴∠CDE = ∠GDF。在△CDE与△GDF中,
$\begin{cases}$
DC = DG, \\
∠CDE = ∠GDF, \\
DE = DF,
$\end{cases}$
∴△CDE≌△GDF(SAS),
∴CE = GF,
∴CE + CD = GF + CG = CF
(3)CD + CF = CE


查看更多完整答案,请扫码查看


