2025年自主学习能力测评单元测试八年级数学上册人教版A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年自主学习能力测评单元测试八年级数学上册人教版A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
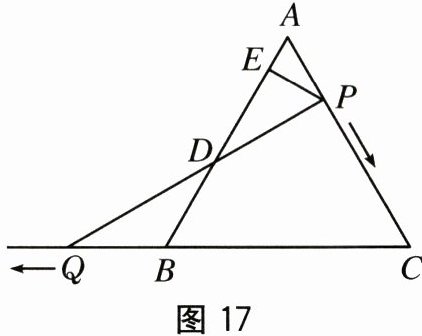
22. (12 分)如图 17,$ \triangle ABC $ 是边长为 6 的等边三角形,$ P $ 是 $ AC $ 边上一动点,由 $ A $ 向 $ C $ 运动(与 $ A,C $ 不重合),$ Q $ 是 $ CB $ 延长线上一点,与点 $ P $ 同时以相同的速度由 $ B $ 向 $ CB $ 延长线方向运动($ Q $ 不与 $ B $ 重合),过点 $ P $ 作 $ PE \perp AB $ 于点 $ E $,连接 $ PQ $ 交 $ AB $ 于点 $ D $.
(1)当 $ \angle BQD = 30^{\circ} $时,求 $ AP $ 的长.
(2)求证:在运动过程中,点 $ D $ 是线段 $ PQ $ 的中点.
(3)在运动过程中线段 $ ED $ 的长是否发生变化? 如果不变,求出线段 $ ED $ 的长;如果变化,说明理由.
(1)当 $ \angle BQD = 30^{\circ} $时,求 $ AP $ 的长.
(2)求证:在运动过程中,点 $ D $ 是线段 $ PQ $ 的中点.
(3)在运动过程中线段 $ ED $ 的长是否发生变化? 如果不变,求出线段 $ ED $ 的长;如果变化,说明理由.

答案:
22.
(1)设AP = x,则BQ = AP = x,
∵∠BQD = 30°,∠C = 60°,
∴∠QPC = 90°,
∴QC = 2PC,即x + 6 = 2(6 - x),解得x = 2。
∴AP = 2
(2)如答图9,过点P作PF//BC交AB于点F,
∴∠PFA = ∠ABC = 60°,∠FPA = ∠ACB = 60°。又∠A = 60°,
∴FP = AP = AF。
∵BQ = AP,
∴FP = BQ。
∵PF//BC,
∴∠FPD = ∠BQD。在△DPF和△DQB中,$\begin{cases}∠FDP = ∠BDQ,\\∠FPD = ∠BQD,\\FP = BQ,\end{cases}$
∴△DPF≌△DQB(AAS)。
∴DP = DQ。
∴点D是PQ的中点

(3)不发生变化。理由如下:
∵PF = AP = AF,PE⊥AF,
∴EF = AE = $\frac{1}{2}$AF。又
∵△DPF ≌△DQB,
∴DF = DB,即DF = $\frac{1}{2}$BF。
∴ED = EF + DF = $\frac{1}{2}$AF + $\frac{1}{2}$BF = $\frac{1}{2}$AB = 3
22.
(1)设AP = x,则BQ = AP = x,
∵∠BQD = 30°,∠C = 60°,
∴∠QPC = 90°,
∴QC = 2PC,即x + 6 = 2(6 - x),解得x = 2。
∴AP = 2
(2)如答图9,过点P作PF//BC交AB于点F,
∴∠PFA = ∠ABC = 60°,∠FPA = ∠ACB = 60°。又∠A = 60°,
∴FP = AP = AF。
∵BQ = AP,
∴FP = BQ。
∵PF//BC,
∴∠FPD = ∠BQD。在△DPF和△DQB中,$\begin{cases}∠FDP = ∠BDQ,\\∠FPD = ∠BQD,\\FP = BQ,\end{cases}$
∴△DPF≌△DQB(AAS)。
∴DP = DQ。
∴点D是PQ的中点

(3)不发生变化。理由如下:
∵PF = AP = AF,PE⊥AF,
∴EF = AE = $\frac{1}{2}$AF。又
∵△DPF ≌△DQB,
∴DF = DB,即DF = $\frac{1}{2}$BF。
∴ED = EF + DF = $\frac{1}{2}$AF + $\frac{1}{2}$BF = $\frac{1}{2}$AB = 3
23. (12 分)数学课上,王老师以“两条线段和的最小值”为题,把“两点之间,线段最短”以及 “垂线段最短”两个知识融合在一起展开一节探究活动课.
【活动一】情境再现,明晰原理
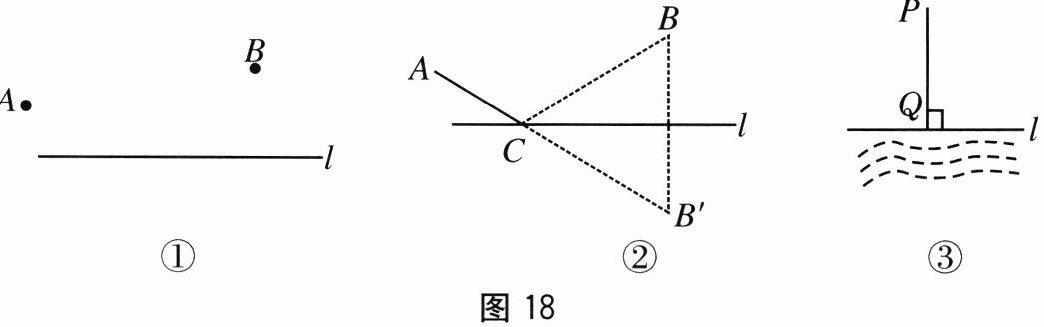
(1)示例 1:将最短路径问题(有人称“将军饮马”问题)转化为数学问题. 如图 18①,用直线 $ l $ 表示河岸,将军从山脚下的点 $ A $ 出发,到达河岸点 $ C $ 饮马后回到点 $ B $ 宿营,怎样走使他每天所走的总路程最短?
作法:如图 18②,作点 $ B $ 关于直线 $ l $ 的对称点 $ B^{\prime} $,连接 $ AB^{\prime} $与直线 $ l $ 交于点 $ C $,则点 $ C $ 即为饮马的地方,此时将军从点 $ A $ 走到点 $ C $,再回到点 $ B $ 所走的总路程最短. 这样做所蕴含的数学原理是
(2)示例 2:如图 18③,要在河岸 $ l $ 上建一座水泵房 $ Q $,修建引水渠从 $ Q $ 到村庄 $ P $ 处.施工人员的做法:过点 $ P $ 作 $ PQ \perp l $ 于点 $ Q $,将水泵房建在 $ Q $ 处,这样修建引水渠 $ PQ $ 最短,既省人力又省物力. 这样做所蕴含的数学原理是
【活动二】感悟方法,尝试应用
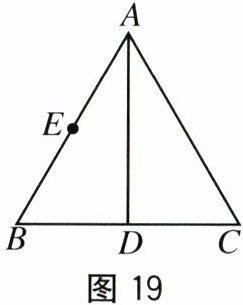
(3)如图 19,在等边三角形 $ ABC $ 中,$ AD $ 是 $ \triangle ABC $ 的中线,且 $ AD = 4 $,点 $ E $ 为 $ AB $ 边的中点,点 $ F $ 为 $ AD $ 上一点,当 $ BF + EF $ 的值最小时,在图 19 上标注点 $ F $ 的位置,并求 $ BF + EF $ 的最小值.
【活动三】迁移拓展,综合应用
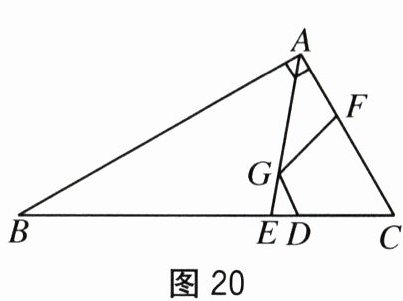
(4)如图 20,在 $ Rt \triangle ABC $ 中,$ \angle B = 30^{\circ} $,点 $ D $ 在斜边 $ BC $ 上,且 $ BC = 4CD = 4 $,$ AE $ 是 $ \angle BAC $ 的平分线,点 $ F,G $ 分别为 $ AC,AE $ 上一点,求 $ DG + FG $ 的最小值.
【活动一】情境再现,明晰原理
(1)示例 1:将最短路径问题(有人称“将军饮马”问题)转化为数学问题. 如图 18①,用直线 $ l $ 表示河岸,将军从山脚下的点 $ A $ 出发,到达河岸点 $ C $ 饮马后回到点 $ B $ 宿营,怎样走使他每天所走的总路程最短?
作法:如图 18②,作点 $ B $ 关于直线 $ l $ 的对称点 $ B^{\prime} $,连接 $ AB^{\prime} $与直线 $ l $ 交于点 $ C $,则点 $ C $ 即为饮马的地方,此时将军从点 $ A $ 走到点 $ C $,再回到点 $ B $ 所走的总路程最短. 这样做所蕴含的数学原理是
两点之间,线段最短
.(2)示例 2:如图 18③,要在河岸 $ l $ 上建一座水泵房 $ Q $,修建引水渠从 $ Q $ 到村庄 $ P $ 处.施工人员的做法:过点 $ P $ 作 $ PQ \perp l $ 于点 $ Q $,将水泵房建在 $ Q $ 处,这样修建引水渠 $ PQ $ 最短,既省人力又省物力. 这样做所蕴含的数学原理是
垂线段最短
.【活动二】感悟方法,尝试应用
(3)如图 19,在等边三角形 $ ABC $ 中,$ AD $ 是 $ \triangle ABC $ 的中线,且 $ AD = 4 $,点 $ E $ 为 $ AB $ 边的中点,点 $ F $ 为 $ AD $ 上一点,当 $ BF + EF $ 的值最小时,在图 19 上标注点 $ F $ 的位置,并求 $ BF + EF $ 的最小值.
【活动三】迁移拓展,综合应用
(4)如图 20,在 $ Rt \triangle ABC $ 中,$ \angle B = 30^{\circ} $,点 $ D $ 在斜边 $ BC $ 上,且 $ BC = 4CD = 4 $,$ AE $ 是 $ \angle BAC $ 的平分线,点 $ F,G $ 分别为 $ AC,AE $ 上一点,求 $ DG + FG $ 的最小值.



答案:
23.
(1)两点之间,线段最短
(2)垂线段最短
(3)如答图10所示,点F为所求。理由如下:
∵点E为AB边的中点,
∴CE是△ABC的中线。
∵△ABC是等边三角形,AD是△ABC的中线,且AD = 4,
∴CE = AD = 4。
∵点B关于AD的对称点为C,
∴BF = CF,
∴BF + EF = CF + EF = CE = 4,即BF + EF的最小值为4

(4)作点F关于AE的对称点F',如答图11所示,由于AE为∠BAC的平分线,则点F'落在AB上,连接DF'交AE于点G,当DF'⊥AB时,DG + FG = DG + F'G = DF'最小。在Rt△BDF'中,BD = 4 - 1 = 3,∠B = 30°,则DF' = $\frac{3}{2}$

23.
(1)两点之间,线段最短
(2)垂线段最短
(3)如答图10所示,点F为所求。理由如下:
∵点E为AB边的中点,
∴CE是△ABC的中线。
∵△ABC是等边三角形,AD是△ABC的中线,且AD = 4,
∴CE = AD = 4。
∵点B关于AD的对称点为C,
∴BF = CF,
∴BF + EF = CF + EF = CE = 4,即BF + EF的最小值为4

(4)作点F关于AE的对称点F',如答图11所示,由于AE为∠BAC的平分线,则点F'落在AB上,连接DF'交AE于点G,当DF'⊥AB时,DG + FG = DG + F'G = DF'最小。在Rt△BDF'中,BD = 4 - 1 = 3,∠B = 30°,则DF' = $\frac{3}{2}$

查看更多完整答案,请扫码查看


