2025年自主学习能力测评单元测试八年级数学上册人教版A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年自主学习能力测评单元测试八年级数学上册人教版A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (10分)课间,小明不小心将等腰直角三角尺教具弄到两墙之间,如图20所示,AD⊥DE,BE⊥DE,∠ACB=90°,AC=CB.
(1)求证△ADC≌△CEB.
(2)若DE=42cm,请你求出砌墙砖块的厚度a的大小(假设每块砖的厚度相等).

(1)求证△ADC≌△CEB.
(2)若DE=42cm,请你求出砌墙砖块的厚度a的大小(假设每块砖的厚度相等).

答案:
21.
(1)
∵AD⊥DE,BE⊥DE,
∴∠ADC = ∠CEB = 90°. 又
∵∠ACB = 90°,
∴∠ACD + ∠ECB = 90°. 又
∵∠ACD + ∠DAC = 90°,
∴∠DAC = ∠ECB. 在$\begin{cases} \angle ADC = \angle CEB, \\ \angle DAC = \angle ECB, \\ AC = CB, \end{cases}$△ADC和△CEB中,
∴△ADC≌△CEB(AAS)
(2)由题意得AD = 4a,BE = 3a,由
(1)得△ADC≌△CEB,
∴DC = BE = 3a,AD = CE = 4a,
∴DC + CE = BE + AD = 7a = 42,
∴a = 6.
∴砌墙砖块的厚度a为6cm
(1)
∵AD⊥DE,BE⊥DE,
∴∠ADC = ∠CEB = 90°. 又
∵∠ACB = 90°,
∴∠ACD + ∠ECB = 90°. 又
∵∠ACD + ∠DAC = 90°,
∴∠DAC = ∠ECB. 在$\begin{cases} \angle ADC = \angle CEB, \\ \angle DAC = \angle ECB, \\ AC = CB, \end{cases}$△ADC和△CEB中,
∴△ADC≌△CEB(AAS)
(2)由题意得AD = 4a,BE = 3a,由
(1)得△ADC≌△CEB,
∴DC = BE = 3a,AD = CE = 4a,
∴DC + CE = BE + AD = 7a = 42,
∴a = 6.
∴砌墙砖块的厚度a为6cm
22. (12分)综合与实践.
【提出问题】课外兴趣小组活动时,老师提出了如下问题:如图21,在△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
【解决问题】小明在组内经过合作交流,得到了如下的解决方法:延长线段AD至点E,使DE=AD,连接BE,如图21.请回答问题:
(1)△ADC≌△EDB的依据是
(2)探究得出AD的取值范围是(
A. 6<AD<8
B. 6≤AD≤8
C. 1<AD<7
D. 1≤AD≤7
【方法感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【方法应用】(3)如图22,已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证∠C=∠BAE.
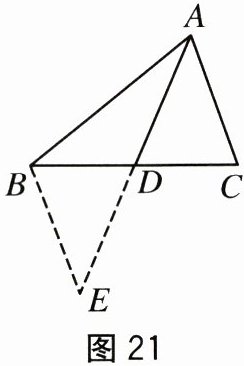

【提出问题】课外兴趣小组活动时,老师提出了如下问题:如图21,在△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
【解决问题】小明在组内经过合作交流,得到了如下的解决方法:延长线段AD至点E,使DE=AD,连接BE,如图21.请回答问题:
(1)△ADC≌△EDB的依据是
SAS
(填符号简写形式).(2)探究得出AD的取值范围是(
C
).A. 6<AD<8
B. 6≤AD≤8
C. 1<AD<7
D. 1≤AD≤7
【方法感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【方法应用】(3)如图22,已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证∠C=∠BAE.


答案:
22.
(1)SAS.提示:
∵AD是△ABC的中线,
∴BD = CD,在$\begin{cases} AD = ED, \\ \angle ADC = \angle EDB, \\ CD = BD, \end{cases}$△ADC与△EDB中,
∴△ADC≌△EDB(SAS),故答案为SAS
(2)C;提示:由
(1)知△ADC≌△EDB,
∴BE = AC = 6,AE = 2AD,由三角形三边之间的关系可得AB - BE < AE < AB + BE,即8 - 6 < 2AD < 8 + 6,解得1 < AD < 7,故选C
(3)延长AE到点F,使EF = AE,连接DF,如答图6所示,
∵AE是△ABD的中线,
∴BE = DE,在△ABE与△FDE中,$\begin{cases} AE = FE, \\ \angle AEB = \angle FED, \\ BE = DE, \end{cases}$
∴△ABE≌△FDE(SAS),
∴AB = FD, ∠BAE = ∠F.
∵CD = AB,
∴CD = FD,
∵∠BAE = ∠F,
∴AB//FD.
∴∠BAD + ∠ADF = 180°.
∵∠BDA + ∠ADC = 180°,∠BDA = ∠BAD,
∴∠ADF = ∠ADC.
∵在△ADF和△ADC中,$\begin{cases} AD = AD, \\ \angle ADF = \angle ADC, \\ FD = CD, \end{cases}$
∴△ADF≌△ADC(SAS),
∴∠F = ∠C,
∴∠C = ∠BAE

22.
(1)SAS.提示:
∵AD是△ABC的中线,
∴BD = CD,在$\begin{cases} AD = ED, \\ \angle ADC = \angle EDB, \\ CD = BD, \end{cases}$△ADC与△EDB中,
∴△ADC≌△EDB(SAS),故答案为SAS
(2)C;提示:由
(1)知△ADC≌△EDB,
∴BE = AC = 6,AE = 2AD,由三角形三边之间的关系可得AB - BE < AE < AB + BE,即8 - 6 < 2AD < 8 + 6,解得1 < AD < 7,故选C
(3)延长AE到点F,使EF = AE,连接DF,如答图6所示,
∵AE是△ABD的中线,
∴BE = DE,在△ABE与△FDE中,$\begin{cases} AE = FE, \\ \angle AEB = \angle FED, \\ BE = DE, \end{cases}$
∴△ABE≌△FDE(SAS),
∴AB = FD, ∠BAE = ∠F.
∵CD = AB,
∴CD = FD,
∵∠BAE = ∠F,
∴AB//FD.
∴∠BAD + ∠ADF = 180°.
∵∠BDA + ∠ADC = 180°,∠BDA = ∠BAD,
∴∠ADF = ∠ADC.
∵在△ADF和△ADC中,$\begin{cases} AD = AD, \\ \angle ADF = \angle ADC, \\ FD = CD, \end{cases}$
∴△ADF≌△ADC(SAS),
∴∠F = ∠C,
∴∠C = ∠BAE

23. (12分)实践与探究.
如图23,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知∠BAD=∠C.
(1)探究:如图24,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证△ABD≌△CAF.
(2)证明:如图25,点B,C在∠MAN的边AM,AN上,点E,F在∠MAN内部的射线AD上,∠1,∠2分别是△ABE,△CAF的外角.已知AB=AC,∠1=∠2=∠BAC. 求证△ABE≌△CAF.
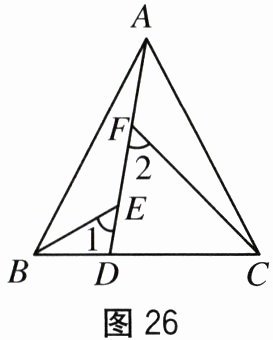
(3)应用:如图26,在△ABC中,AB=AC,AB>BC. 点D在边BC上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC. 若△ABC的面积为15,求△ACF与△BDE的面积之和.
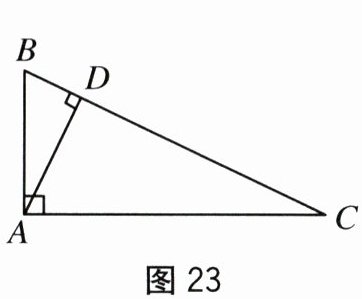


如图23,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知∠BAD=∠C.
(1)探究:如图24,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证△ABD≌△CAF.
(2)证明:如图25,点B,C在∠MAN的边AM,AN上,点E,F在∠MAN内部的射线AD上,∠1,∠2分别是△ABE,△CAF的外角.已知AB=AC,∠1=∠2=∠BAC. 求证△ABE≌△CAF.
(3)应用:如图26,在△ABC中,AB=AC,AB>BC. 点D在边BC上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC. 若△ABC的面积为15,求△ACF与△BDE的面积之和.




答案:
23.
(1)
∵∠MAN = 90°,CF⊥AE,BD⊥AE,
∴∠MAN = ∠AFC = ∠BDA = 90°.
∴∠DBA + ∠BAD = 90°,∠BAD + ∠FAC = 90°,
∴∠DBA = ∠FAC.在△ABD和△CAF中,$\begin{cases} \angle BDA = \angle AFC, \\ \angle DBA = \angle FAC, \\ AB = CA, \end{cases}$
∴△ABD≌△CAF(AAS)
(2)
∵∠1 = ∠2 = ∠BAC,∠1 = ∠EBA + ∠EAB,∠BAC = ∠EAB + ∠FAC,
∴∠EBA = ∠FAC,∠BEA = 180° - ∠1 = 180° - ∠2 = ∠AFC. 在$\begin{cases} \angle BEA = \angle AFC, \\ \angle EBA = \angle FAC, \\ AB = CA, \end{cases}$△ABE和△CAF中,
∴△ABE≌△CAF(AAS)
(3)
∵∠1 = ∠2 = ∠BAC,∠1 = ∠EBA + ∠EAB,∠BAC = ∠EAB + ∠FAC,
∴∠EBA = ∠FAC,∠BEA = 180° - ∠1 = 180° - ∠2 = ∠AFC. 在$\begin{cases} \angle BEA = \angle AFC, \\ \angle EBA = \angle FAC, \\ AB = CA, \end{cases}$△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
∴$S_{\triangle ABE} = S_{\triangle CAF}$.
∵CD = 2BD,
∴$BD = \frac{1}{3}BC$,
∴$S_{\triangle ABD} = \frac{1}{3}S_{\triangle ABC} = \frac{1}{3} × 15$ = 5,
∴$S_{\triangle ACF} + S_{\triangle BDE} = S_{\triangle ABE} + S_{\triangle BDE} = S_{\triangle ABD} = 5$
(1)
∵∠MAN = 90°,CF⊥AE,BD⊥AE,
∴∠MAN = ∠AFC = ∠BDA = 90°.
∴∠DBA + ∠BAD = 90°,∠BAD + ∠FAC = 90°,
∴∠DBA = ∠FAC.在△ABD和△CAF中,$\begin{cases} \angle BDA = \angle AFC, \\ \angle DBA = \angle FAC, \\ AB = CA, \end{cases}$
∴△ABD≌△CAF(AAS)
(2)
∵∠1 = ∠2 = ∠BAC,∠1 = ∠EBA + ∠EAB,∠BAC = ∠EAB + ∠FAC,
∴∠EBA = ∠FAC,∠BEA = 180° - ∠1 = 180° - ∠2 = ∠AFC. 在$\begin{cases} \angle BEA = \angle AFC, \\ \angle EBA = \angle FAC, \\ AB = CA, \end{cases}$△ABE和△CAF中,
∴△ABE≌△CAF(AAS)
(3)
∵∠1 = ∠2 = ∠BAC,∠1 = ∠EBA + ∠EAB,∠BAC = ∠EAB + ∠FAC,
∴∠EBA = ∠FAC,∠BEA = 180° - ∠1 = 180° - ∠2 = ∠AFC. 在$\begin{cases} \angle BEA = \angle AFC, \\ \angle EBA = \angle FAC, \\ AB = CA, \end{cases}$△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
∴$S_{\triangle ABE} = S_{\triangle CAF}$.
∵CD = 2BD,
∴$BD = \frac{1}{3}BC$,
∴$S_{\triangle ABD} = \frac{1}{3}S_{\triangle ABC} = \frac{1}{3} × 15$ = 5,
∴$S_{\triangle ACF} + S_{\triangle BDE} = S_{\triangle ABE} + S_{\triangle BDE} = S_{\triangle ABD} = 5$
查看更多完整答案,请扫码查看


