2025年自主学习能力测评单元测试八年级数学上册人教版A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年自主学习能力测评单元测试八年级数学上册人教版A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
17. (8 分)如图 12,一艘轮船位于灯塔 $ P $ 的南偏东 $ 30^{\circ} $方向的 $ M $ 处,它以 $ 20 n mile/h $(海里/时,$ 1 n mile = 1852 m $)的速度向正北方向航行,2 h 后到达灯塔 $ P $ 的北偏东 $ 60^{\circ} $方向的 $ N $ 处,求此时 $ N $ 处与灯塔 $ P $ 的距离.


答案:
17.依题意,得AB//MN,MN = 2×20 = 40(n mile),
∵∠BPM = 30°,∠APN = 60°,
∴∠M = ∠BPM = 30°,∠NPM = 180° - ∠BPM - ∠APN = 180° - 30° - 60° = 90°。在Rt△PMN中,∠M = 30°,
∴NP = $\frac{1}{2}$MN = 20(n mile)
∵∠BPM = 30°,∠APN = 60°,
∴∠M = ∠BPM = 30°,∠NPM = 180° - ∠BPM - ∠APN = 180° - 30° - 60° = 90°。在Rt△PMN中,∠M = 30°,
∴NP = $\frac{1}{2}$MN = 20(n mile)
18. (10 分)如图 13,在 $ 7 × 7 $ 的网格中,每个小正方形的边长都为 1 个单位长度.
(1)请在网格平面内,画出平面直角坐标系,使点 $ A,B $ 的坐标分别为 $ A(1,3),B(-2,-1) $,并直接写出点 $ C $ 的坐标.
(2)作出 $ \triangle ABC $ 关于 $ y $ 轴对称的 $ \triangle A^{\prime}B^{\prime}C^{\prime} $.
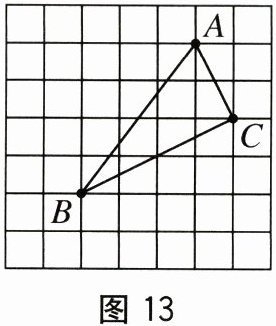
(1)请在网格平面内,画出平面直角坐标系,使点 $ A,B $ 的坐标分别为 $ A(1,3),B(-2,-1) $,并直接写出点 $ C $ 的坐标.
(2)作出 $ \triangle ABC $ 关于 $ y $ 轴对称的 $ \triangle A^{\prime}B^{\prime}C^{\prime} $.

答案:
18.
(1)如答图7所示,平面直角坐标系为所求。C(2,1)
(2)如答图7所示,△A'B'C'为所求
(1)如答图7所示,平面直角坐标系为所求。C(2,1)
(2)如答图7所示,△A'B'C'为所求
19. (10 分)如图 14,在 $ \triangle ABC $ 中,$ AC < AB < BC $.
(1)尺规作图:请在图 14 中,作线段 $ AB $ 的垂直平分线,交 $ AB $ 于点 $ Q $,交 $ BC $ 于点 $ P $.
(2)连接 $ AP $,若 $ \angle B = 25^{\circ} $,则 $ \angle APC = $
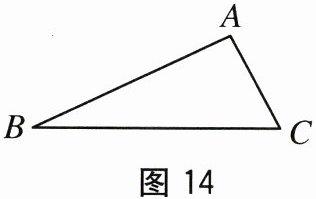
(1)尺规作图:请在图 14 中,作线段 $ AB $ 的垂直平分线,交 $ AB $ 于点 $ Q $,交 $ BC $ 于点 $ P $.
(2)连接 $ AP $,若 $ \angle B = 25^{\circ} $,则 $ \angle APC = $
50°
.
答案:
19.
(1)如答图8所示,直线PQ即为所求

(2)连接AP,如答图8。
∵PQ是AB的垂直平分线,
∴BP = AP,
∴∠ABP = ∠BAP = 25°,∠APC = ∠ABP + ∠BAP = 50°
19.
(1)如答图8所示,直线PQ即为所求

(2)连接AP,如答图8。
∵PQ是AB的垂直平分线,
∴BP = AP,
∴∠ABP = ∠BAP = 25°,∠APC = ∠ABP + ∠BAP = 50°
20. (10 分)如图 15,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD \perp BC $ 于点 $ D $,$ AM $ 是 $ \triangle ABC $ 的外角 $ \angle EAC $ 的平分线.
(1)求证 $ AM // BC $.
(2)若 $ DN $ 平分 $ \angle ADC $ 交 $ AM $ 于点 $ N $,判断 $ \triangle ADN $ 的形状,并说明理由.
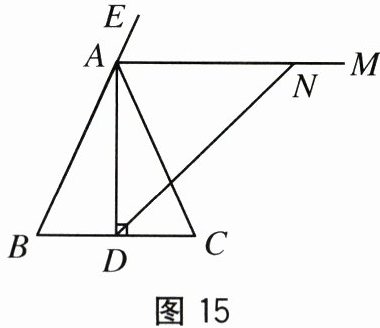
(1)求证 $ AM // BC $.
(2)若 $ DN $ 平分 $ \angle ADC $ 交 $ AM $ 于点 $ N $,判断 $ \triangle ADN $ 的形状,并说明理由.

答案:
20.
(1)
∵AB = AC,AD⊥BC,
∴∠BAD = ∠CAD = $\frac{1}{2}$∠BAC。
∵AM平分∠EAC,
∴∠EAM = ∠MAC = $\frac{1}{2}$∠EAC。
∴∠MAD = ∠MAC + ∠CAD = $\frac{1}{2}$(∠EAC + ∠BAC) = $\frac{1}{2}$×180° = 90°。
∵AD⊥BC,
∴∠ADC = 90°。
∴∠MAD + ∠ADC = 180°,
∴AM//BC
(2)△ADN是等腰直角三角形。理由如下:
∵AM//BC,
∴∠AND = ∠NDC。
∵DN平分∠ADC,
∴∠ADN = ∠NDC = $\frac{1}{2}$∠ADC = 45°。
∴∠AND = ∠ADN,
∴AD = AN,
∴△ADN是等腰三角形。又∠NAD = 90°,
∴△ADN是等腰直角三角形
(1)
∵AB = AC,AD⊥BC,
∴∠BAD = ∠CAD = $\frac{1}{2}$∠BAC。
∵AM平分∠EAC,
∴∠EAM = ∠MAC = $\frac{1}{2}$∠EAC。
∴∠MAD = ∠MAC + ∠CAD = $\frac{1}{2}$(∠EAC + ∠BAC) = $\frac{1}{2}$×180° = 90°。
∵AD⊥BC,
∴∠ADC = 90°。
∴∠MAD + ∠ADC = 180°,
∴AM//BC
(2)△ADN是等腰直角三角形。理由如下:
∵AM//BC,
∴∠AND = ∠NDC。
∵DN平分∠ADC,
∴∠ADN = ∠NDC = $\frac{1}{2}$∠ADC = 45°。
∴∠AND = ∠ADN,
∴AD = AN,
∴△ADN是等腰三角形。又∠NAD = 90°,
∴△ADN是等腰直角三角形
21. (10 分)如图 16,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle BAC = 90^{\circ} $,$ M $ 是 $ BC $ 的中点,点 $ E,F $ 分别在 $ AB,AC $ 边上,且 $ BE = AF $,连接 $ EM,FM $. 求证
(1)$ EM = FM $.
(2)$ EM \perp FM $.
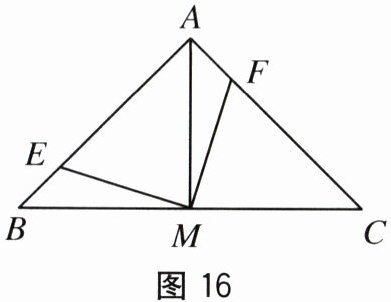
(1)$ EM = FM $.
(2)$ EM \perp FM $.

答案:
21.
(1)
∵AB = AC,∠BAC = 90°,
∴∠B = ∠C = 45°。
∵AB = AC,点M是BC的中点,
∴∠BAM = ∠CAM = $\frac{1}{2}$∠BAC = 45°。
∴∠B = ∠BAM = ∠CAM = 45°。
∵∠B = ∠BAM,
∴BM = AM。在△BEM和△AFM中,$\begin{cases}BE = AF,\\∠B = ∠FAM,\end{cases}$
∴△BEM≌△AFM(SAS),
∴EM = FM
(2)由
(1),得△BEM≌△AFM,
∴∠BME = ∠AMF。
∵∠AMB = 90°,
∴∠AME + ∠BME = 90°。
∴∠AMF + ∠AME = 90°,
∴∠EMF = 90°,
∴EM⊥FM
(1)
∵AB = AC,∠BAC = 90°,
∴∠B = ∠C = 45°。
∵AB = AC,点M是BC的中点,
∴∠BAM = ∠CAM = $\frac{1}{2}$∠BAC = 45°。
∴∠B = ∠BAM = ∠CAM = 45°。
∵∠B = ∠BAM,
∴BM = AM。在△BEM和△AFM中,$\begin{cases}BE = AF,\\∠B = ∠FAM,\end{cases}$
∴△BEM≌△AFM(SAS),
∴EM = FM
(2)由
(1),得△BEM≌△AFM,
∴∠BME = ∠AMF。
∵∠AMB = 90°,
∴∠AME + ∠BME = 90°。
∴∠AMF + ∠AME = 90°,
∴∠EMF = 90°,
∴EM⊥FM
查看更多完整答案,请扫码查看


