2025年自主学习能力测评单元测试八年级数学上册人教版A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年自主学习能力测评单元测试八年级数学上册人教版A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
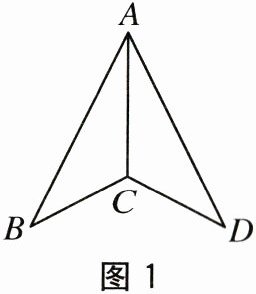
1.如图1,△ABC≌△ADC,则与AB长度相等的线段是().
A.DC
B.AC
C.BC
D.AD
A.DC
B.AC
C.BC
D.AD
答案:
D
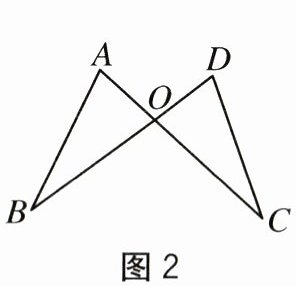
2.如图2,已知AB=DC,那么要得到△ABO≌△DCO,还需要增加的条件是().
A.AO=DO
B.BO=CO
C.∠A=∠D
D.∠A=∠B
A.AO=DO
B.BO=CO
C.∠A=∠D
D.∠A=∠B
答案:
C
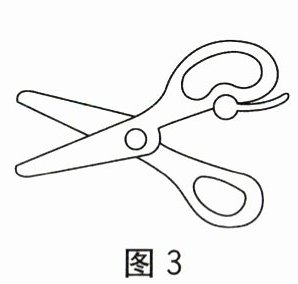
3.如图3是一把剪刀,把它抽象为图4,其中OA=OB.若剪刀张开的角为30°,则∠A的
度数为().
A.30°
B.60°
C.75°
D.85°
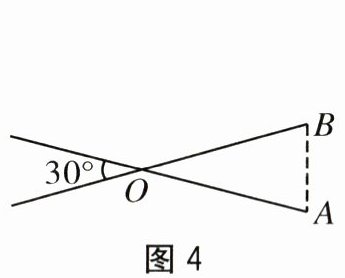
度数为().

A.30°
B.60°
C.75°
D.85°

答案:
C
4.如图5,AC=AD,BC=BD,则有().
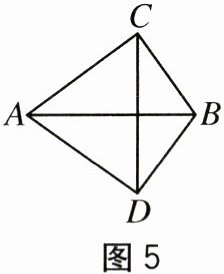
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB

A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
答案:
A
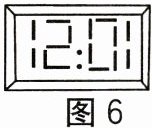
5.如图6,图中显示的是从镜子中看到背后墙上的电子钟读数,由此你可以推
断这时的实际时间是().
A.12:01 B.10:21 C.10:51 D.10:01
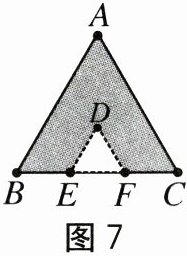
6.如图7,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分
别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长
是().
A.4 B.6 C.8 D.12
7.为测量一池塘两端A,B之间的距离,两名同学分别设计了以下两种不同
的方案.
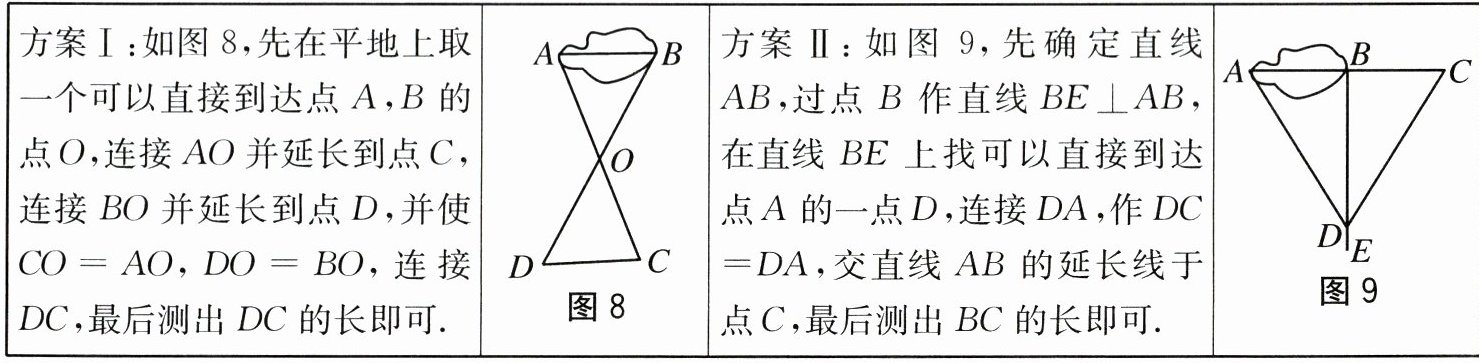
则以下说法正确的是().
A.方案I、II都不可行 B.方案I、II都可行
C.方案I可行,方案II不可行 D.方案I不可行,方案II可行
8.如图10,在△ABC中,AB=AC,∠A=30°,以点B为圆心,BC的长为半径画弧,交
AC于点D,连接BD,则∠ABD的度数为().
A.60° B.45° C.40° D.30°
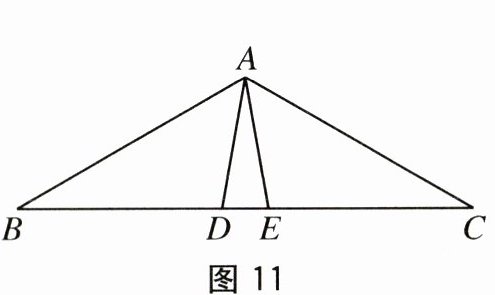
9.如图11,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的
是().
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠DAE=40° D.∠C=30°
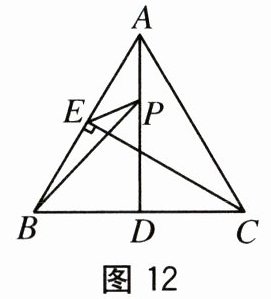
10.如图12,在等边△ABC中,AD是△ABC的中线,CE⊥AB,AD=5,P是AD上一个
动点,则PB十PE的最小值是().
A.2.5 B.5 C.7.5 D.10
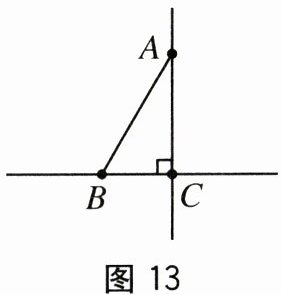
11.如图13,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使
得△PAB为等腰三角形,则符合条件的点P共有().
A.4个 B.5个 C.6个 D.7个
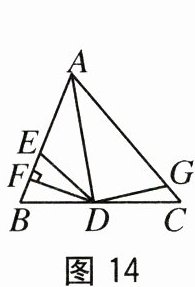
12.如图14,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG与
△AED的面积分别为27和16,则△EDF的面积为().
A.3.5 B.5.5 C.7 D.11
二、填空题(共4小题,每小题3分,共12分)
13.已知等腰三角形的底边长为2,腰长为8,则它的周长为.
14.已知△ABC≌△DEF,△ABC的周长为100cm,DE=30cm,DF=
25cm,那么BC=cm.
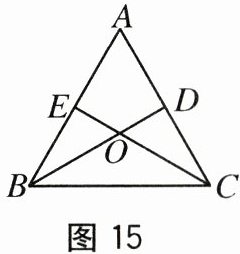
15.如图15,等边三角形ABC的两条角平分线BD和CE交于点O,则
∠BOC的度数为.
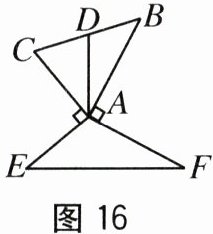
16.如图16,AD是△ABC的中线,AE⊥AC,AF⊥AB,且AE=AC,AF=
AB.若AD=3,则EF的长为.
三、解答题(共7小题,共72分.解答应写出文字说明、证明过程或演算步骤)
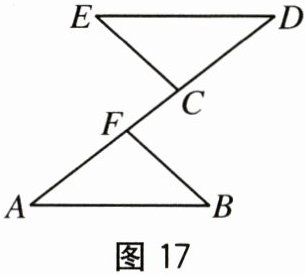
17.(8分)已知,如图17,A,F,C,D四点在一直线上,AC=DF,∠A=∠D,且AB=DE.
求证
(1)△ABF≌△DEC.
(2)EC//BF.
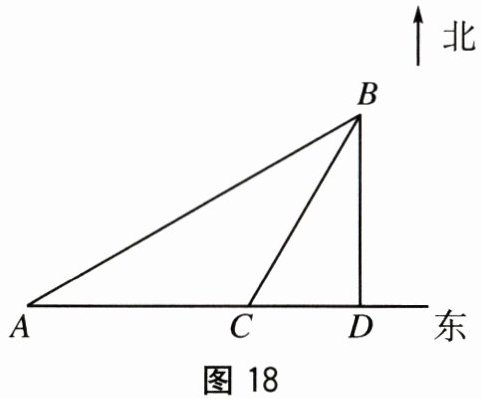
18.(10分)如图18,某船在上午11时30分在A处观测到B
岛在东偏北30°方向,该船以10nmile/h的速度向东航
行到C处,此时观测到B岛在东偏北60°方向,且船距B
岛40nmile.
(1)求船到达C处的时间.
(2)若该船从C处继续向东航行,何时到达B岛正南方向
的D处?
19.(10分)嘉淇同学要证AE=BF,她先用下列尺规作图步骤作图:①AD//BC,∠BAD=
90°;②以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE;③过点C
作CF⊥BE,垂足为点F,并写出如下不完整的已知和求证.
(1)在方框中填空,补全已知和求证.
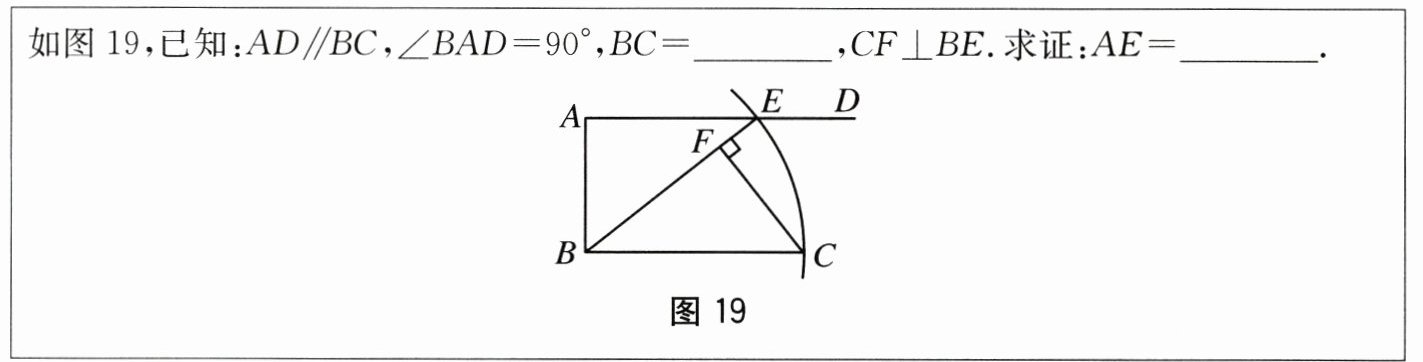
(2)按嘉淇的想法写出证明过程.
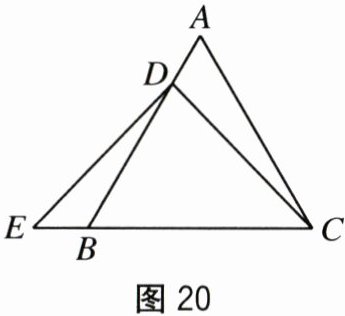
20.(10分)如图20,在等边三角形ABC中,D是AB上的一点,E是
CB延长线上一点,连接CD,DE,已知∠EDB=∠ACD.
(1)求证:△EDC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
21.(10分)综合与实践−−生活中的数学.
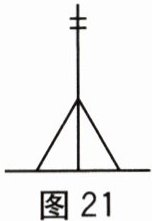
去学校的路上,小陶发现路边的一根电线杆两侧对称地拉着钢绳(如图21),他很快明
白了其中的道理.
[提出问题]小陶来到学校,看到学校的旗杆两侧并没有拉着钢绳,于是他提出问题:学
校的旗杆是否垂直于地面?
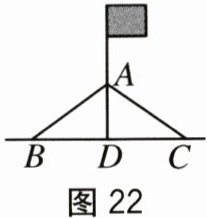
[实践操作]如图22,小陶找来两根5m长的绳子,一端系在旗杆上的同一位置A处,另
一端分别固定在地面的两个木桩B,C上(两个木桩和旗杆在同一平面内,绳结处的长
度误差忽略不计),小陶现只有一把卷尺.
[解决问题](1)如图21,电线杆两侧对称地拉着钢绳是为了防止电线杆倾
倒,这样做是利用了.
(2)如图22,需要用卷尺测量哪些线段的长度?
(3)如图22,当测量出的线段满足什么条件时,旗杆是垂直于地面的?并
说明理由.
22.(12分)实践与探究.
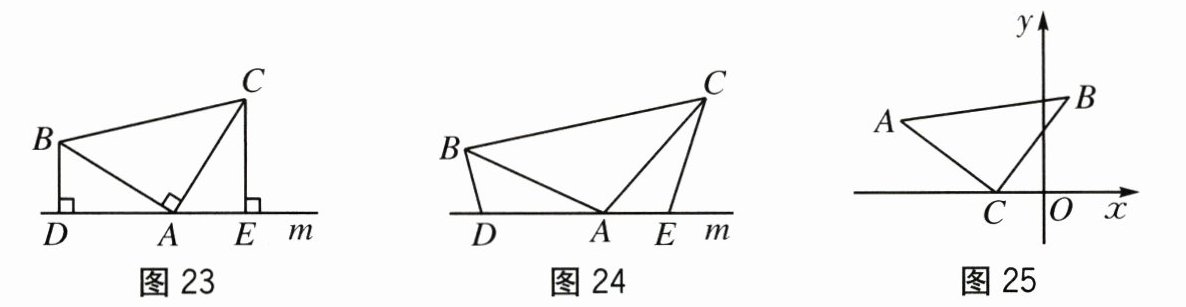
[问题背景](1)如图23,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥
直线m,CE⊥直线m,垂足分别为点D,E.证明:DE=AD+AE=+.
[拓展延伸](2)如图24,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都
在直线m上,并且有∠BDA=∠AEC=∠BAC.写出DE,BD,CE三条线段的数量关
系,并证明.
[实际应用](3)如图25,在△ABC中,∠ACB=90°,AC=BC,点C的坐标为(−2,0),
点A的坐标为(−6,3),直接写出点B的坐标.
23.(12分)探究与证明.
△ABC与△BDE均为等腰直角三角形,∠ABC=∠DBE=90°.
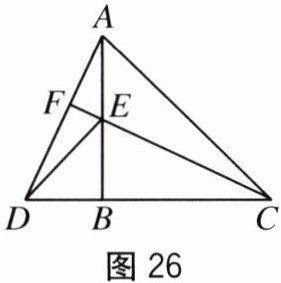
[特例体验](1)如图26,当D,B,C在同一条直线上时,CE的延长线与AD交于点F.
求证:∠CFA=90°.
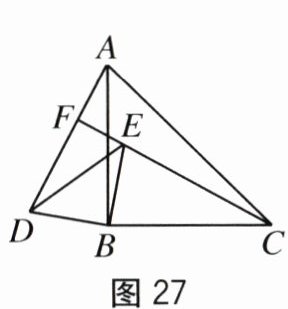
[类比探究](2)当△ABC与△BDE的位置如图27时,CE的延长线与AD交于点F,
猜想∠CFA的大小,并证明你的结论.
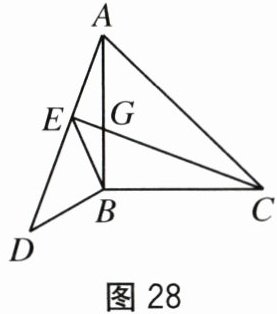
[拓展迁移](3)如图28,当A,E,D在同一条直线上时(A,D在点E的异侧),CE与
AB交于点G,∠BAD=∠ACE,求证:BG+AB=AC.
专项练习(二)
整式的乘法 因式分解 分式
(建议完成时间:120分钟 满分:120分)
注意事项:
1.答题前,务必将班级、姓名、学号填写在练习和答题卡上.
2.作答时,请在答题卡上作答(答题注意事项见答题卡),在本练习上作答无效.
一、单项选择题(在每小题给出的四个选项中只有一项是符合要求的,每小题3分,共36分)
1.7−1的值是().
A.−7 B.7 C.$\frac{1}{7}$ D.−$\frac{1}{7}$
2.下列运算结果正确的是().
A.x3.x4=x12 B.(−2x²)3=−8x6
C.x6÷x3=x² D.x²+x²=x5
3.计算$\frac{m}{m−1}$+$\frac{1}{1−m}$的结果是().
A.1 B.−1 C.2 D.−2
4.经测算,一个水分子的直径约为0.0000000004m,数据0.0000000004用科学记数
法表示为().
A.4×10−11 B.0.4×10−9 C.4×10−9 D.4×10−10
5.已知一个正方形的面积是x²−4x+4(r<2),则这个正方形的边长是().
A.2−x B.x−2 C.4−x D.x−4
6.将分式$\frac{x}{+}$中的x,y的值同时扩大为原来的2倍,则分式的值().
A.缩小为原来的一半 B.扩大为原来的2倍
C.无法确定 D.保持不变
7.甲同学做完四道整式乘法的题后,同桌乙同学的批改如图1所示,则乙同学批改正确的
是().
A.第①、②题 B.第①、④题 C.第②、③题 D.第③、④题
8.一个长方体箱子的长、宽、高分别为2x+2,x,2x,则这个箱子的体积为().
A.4x²+4x B.4x3+4x² C.4x3+4x D.4x²+4
9.将关于x的分式方程$\frac{3}{x−2}$=$\frac{5}{2−x}$−1去分母、去括号后所得整式方程正确的是().
A.3=5−x−2 B.3=−5−x−2
C.3=5−x+2 D.3=−5−x+2
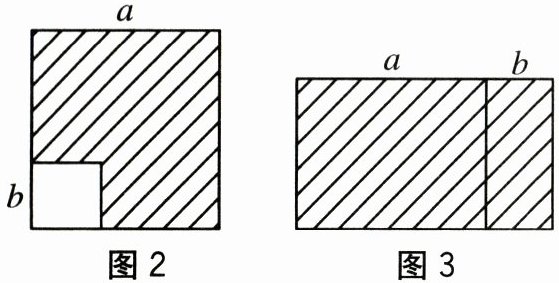
10.在边长为a的正方形中挖掉一个边长为b(a>b)的小正方形(如图2),把余下的部分
剪拼成一个长方形(如图3),通过计算图形(阴影部分,如图3)的面积,验证了一个等
式,则这个等式是().
A.a²−ab=a(a−b)
B.a²−b²=(a+b)(a−b)
C.(a+b)²=a²+2ab+b²
D.(a−b)²=a²−2ab+b²
11.已知(x"+a+xn+b)÷x"+1=x²+x²,其中n是正整数,a−b的值是().
A.−1 B.0 C.1 D.−1或1
12.“孔子周游列国”是流传很广的故事.有一次他和学生到离他们住的驿站30里(里为古
代距离单位)的书院参观,学生步行出发1小时后,孔子坐车出发,车的速度是步行的
1.5倍,孔子和学生们同时到达书院,设学生步行的速度为每小时x里,则可列方程为
().
A.$\frac{30}{x}$=$\frac{30}{1.5x}$+1 B.$\frac{30}{x}$=$\frac{30}{1.5x+1}$
C.$\frac{30}{x}$=$\frac{30}{1.5x}$−1 D.$\frac{30}{x}$=$\frac{30}{1.5x−1}$
二、填空题(共4小题,每小题3分,共12分)
13.若分式$\frac{1}{3−x}$有意义,则x的取值范围是.
14.分解因式:3a²−3=.
15.若9x²+mxy+y²是一个完全平方式,则m=.
16.若mn=−4,m+n=5,则代数式m²n+mn²的值为.
三、解答题(共7小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)利用乘法公式计算下列各题:
(1)2002²;
(2)2024×2026−20252.
18.(8分)解分式方程:$\frac{3−x}{x−4}$+$\frac{1}{4−x}$=1.
19.(10分)关于x的分式方程$\frac{ax−1}{4−x}$+$\frac{27}{x−4}$=−8的解为正数,求a的取值范围.
20.(10分)以下是某同学化简分式($\frac{x+1}{x²−4}$−$\frac{1}{x+2}$)÷$\frac{3}{x−2}$的部分运算过程:
解:原式=$\frac{x+1}{(x+2)(x−2)}$−$\frac{1}{x+2}${.$\frac{x−2}{3}$……第一步
=$\frac{x+1}{(x+2)(x−2)}$−$\frac{x−2}{(x+2)(x−2)}$1.$\frac{x−2}{3}$……第二步
=$\frac{x+1−x−2}{(x+2)(x−2)}$.$\frac{x−2}{3}$……第三步
任务一:填空
(1)以上化简步骤中,第步是通分,通分的依据是.
(2)第步开始出现错误,错误的原因是.
任务二:化简
(3)请写出该分式化简的正确过程.
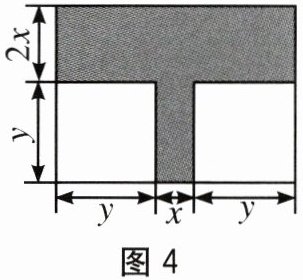
21.(10分)如图4,某中学校园内有一块长为(x+2y)m,宽为(2x十y)m的长方形地块,学
校计划在中间留下一个“T"型的图形(阴影部分)修建一个文化广场.
(1)用含x,y的代数式表示“T'"型图形的面积并化简.
(2)若x=2,y=3,预计修建文化广场每平方米的费用为150元,求
修建文化广场所需要的费用.
22.(12分)金师傅近期准备换车,看中了价格相同的两款国产车
燃油车油箱容积:40L,油价:7元/L,续航里 新能源车电池电量:100kW.h,电价:0.6
程:akm,每千米行驶费用:$\frac{40×7}{a}$元 元费/用(k:W.h),续航里程元:akm,每千米行驶
(1)用含a的代数式表示新能源车每千米行驶费用.
(2)若燃油车每千米行驶费用比新能源车多0.5元.
①分别求出这两款车每千米行驶费用(保留一位小数).
②若燃油车和新能源车每年的其他费用分别为4800元和7500元.每年行驶里程
为多少千米时,买新能源车的年费用更低?(年费用=年行驶费用十年其他费用)
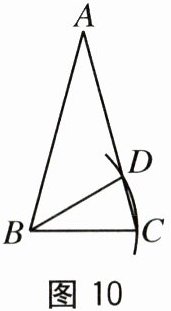

断这时的实际时间是().
A.12:01 B.10:21 C.10:51 D.10:01
6.如图7,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分
别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长
是().
A.4 B.6 C.8 D.12
7.为测量一池塘两端A,B之间的距离,两名同学分别设计了以下两种不同
的方案.

则以下说法正确的是().
A.方案I、II都不可行 B.方案I、II都可行
C.方案I可行,方案II不可行 D.方案I不可行,方案II可行
8.如图10,在△ABC中,AB=AC,∠A=30°,以点B为圆心,BC的长为半径画弧,交
AC于点D,连接BD,则∠ABD的度数为().
A.60° B.45° C.40° D.30°
9.如图11,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的
是().
A.△ABE≌△ACD B.△ABD≌△ACE
C.∠DAE=40° D.∠C=30°
10.如图12,在等边△ABC中,AD是△ABC的中线,CE⊥AB,AD=5,P是AD上一个
动点,则PB十PE的最小值是().
A.2.5 B.5 C.7.5 D.10
11.如图13,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使
得△PAB为等腰三角形,则符合条件的点P共有().
A.4个 B.5个 C.6个 D.7个
12.如图14,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG与
△AED的面积分别为27和16,则△EDF的面积为().
A.3.5 B.5.5 C.7 D.11
二、填空题(共4小题,每小题3分,共12分)
13.已知等腰三角形的底边长为2,腰长为8,则它的周长为.
14.已知△ABC≌△DEF,△ABC的周长为100cm,DE=30cm,DF=
25cm,那么BC=cm.
15.如图15,等边三角形ABC的两条角平分线BD和CE交于点O,则
∠BOC的度数为.
16.如图16,AD是△ABC的中线,AE⊥AC,AF⊥AB,且AE=AC,AF=
AB.若AD=3,则EF的长为.
三、解答题(共7小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)已知,如图17,A,F,C,D四点在一直线上,AC=DF,∠A=∠D,且AB=DE.
求证
(1)△ABF≌△DEC.
(2)EC//BF.
18.(10分)如图18,某船在上午11时30分在A处观测到B
岛在东偏北30°方向,该船以10nmile/h的速度向东航
行到C处,此时观测到B岛在东偏北60°方向,且船距B
岛40nmile.
(1)求船到达C处的时间.
(2)若该船从C处继续向东航行,何时到达B岛正南方向
的D处?
19.(10分)嘉淇同学要证AE=BF,她先用下列尺规作图步骤作图:①AD//BC,∠BAD=
90°;②以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE;③过点C
作CF⊥BE,垂足为点F,并写出如下不完整的已知和求证.
(1)在方框中填空,补全已知和求证.

(2)按嘉淇的想法写出证明过程.
20.(10分)如图20,在等边三角形ABC中,D是AB上的一点,E是
CB延长线上一点,连接CD,DE,已知∠EDB=∠ACD.
(1)求证:△EDC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
21.(10分)综合与实践−−生活中的数学.
去学校的路上,小陶发现路边的一根电线杆两侧对称地拉着钢绳(如图21),他很快明
白了其中的道理.
[提出问题]小陶来到学校,看到学校的旗杆两侧并没有拉着钢绳,于是他提出问题:学
校的旗杆是否垂直于地面?
[实践操作]如图22,小陶找来两根5m长的绳子,一端系在旗杆上的同一位置A处,另
一端分别固定在地面的两个木桩B,C上(两个木桩和旗杆在同一平面内,绳结处的长
度误差忽略不计),小陶现只有一把卷尺.
[解决问题](1)如图21,电线杆两侧对称地拉着钢绳是为了防止电线杆倾
倒,这样做是利用了.
(2)如图22,需要用卷尺测量哪些线段的长度?
(3)如图22,当测量出的线段满足什么条件时,旗杆是垂直于地面的?并
说明理由.
22.(12分)实践与探究.
[问题背景](1)如图23,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥
直线m,CE⊥直线m,垂足分别为点D,E.证明:DE=AD+AE=+.
[拓展延伸](2)如图24,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都
在直线m上,并且有∠BDA=∠AEC=∠BAC.写出DE,BD,CE三条线段的数量关
系,并证明.
[实际应用](3)如图25,在△ABC中,∠ACB=90°,AC=BC,点C的坐标为(−2,0),
点A的坐标为(−6,3),直接写出点B的坐标.
23.(12分)探究与证明.
△ABC与△BDE均为等腰直角三角形,∠ABC=∠DBE=90°.
[特例体验](1)如图26,当D,B,C在同一条直线上时,CE的延长线与AD交于点F.
求证:∠CFA=90°.
[类比探究](2)当△ABC与△BDE的位置如图27时,CE的延长线与AD交于点F,
猜想∠CFA的大小,并证明你的结论.
[拓展迁移](3)如图28,当A,E,D在同一条直线上时(A,D在点E的异侧),CE与
AB交于点G,∠BAD=∠ACE,求证:BG+AB=AC.
专项练习(二)
整式的乘法 因式分解 分式
(建议完成时间:120分钟 满分:120分)
注意事项:
1.答题前,务必将班级、姓名、学号填写在练习和答题卡上.
2.作答时,请在答题卡上作答(答题注意事项见答题卡),在本练习上作答无效.
一、单项选择题(在每小题给出的四个选项中只有一项是符合要求的,每小题3分,共36分)
1.7−1的值是().
A.−7 B.7 C.$\frac{1}{7}$ D.−$\frac{1}{7}$
2.下列运算结果正确的是().
A.x3.x4=x12 B.(−2x²)3=−8x6
C.x6÷x3=x² D.x²+x²=x5
3.计算$\frac{m}{m−1}$+$\frac{1}{1−m}$的结果是().
A.1 B.−1 C.2 D.−2
4.经测算,一个水分子的直径约为0.0000000004m,数据0.0000000004用科学记数
法表示为().
A.4×10−11 B.0.4×10−9 C.4×10−9 D.4×10−10
5.已知一个正方形的面积是x²−4x+4(r<2),则这个正方形的边长是().
A.2−x B.x−2 C.4−x D.x−4
6.将分式$\frac{x}{+}$中的x,y的值同时扩大为原来的2倍,则分式的值().
A.缩小为原来的一半 B.扩大为原来的2倍
C.无法确定 D.保持不变
7.甲同学做完四道整式乘法的题后,同桌乙同学的批改如图1所示,则乙同学批改正确的
是().
A.第①、②题 B.第①、④题 C.第②、③题 D.第③、④题
8.一个长方体箱子的长、宽、高分别为2x+2,x,2x,则这个箱子的体积为().
A.4x²+4x B.4x3+4x² C.4x3+4x D.4x²+4
9.将关于x的分式方程$\frac{3}{x−2}$=$\frac{5}{2−x}$−1去分母、去括号后所得整式方程正确的是().
A.3=5−x−2 B.3=−5−x−2
C.3=5−x+2 D.3=−5−x+2
10.在边长为a的正方形中挖掉一个边长为b(a>b)的小正方形(如图2),把余下的部分
剪拼成一个长方形(如图3),通过计算图形(阴影部分,如图3)的面积,验证了一个等
式,则这个等式是().
A.a²−ab=a(a−b)
B.a²−b²=(a+b)(a−b)
C.(a+b)²=a²+2ab+b²
D.(a−b)²=a²−2ab+b²
11.已知(x"+a+xn+b)÷x"+1=x²+x²,其中n是正整数,a−b的值是().
A.−1 B.0 C.1 D.−1或1
12.“孔子周游列国”是流传很广的故事.有一次他和学生到离他们住的驿站30里(里为古
代距离单位)的书院参观,学生步行出发1小时后,孔子坐车出发,车的速度是步行的
1.5倍,孔子和学生们同时到达书院,设学生步行的速度为每小时x里,则可列方程为
().
A.$\frac{30}{x}$=$\frac{30}{1.5x}$+1 B.$\frac{30}{x}$=$\frac{30}{1.5x+1}$
C.$\frac{30}{x}$=$\frac{30}{1.5x}$−1 D.$\frac{30}{x}$=$\frac{30}{1.5x−1}$
二、填空题(共4小题,每小题3分,共12分)
13.若分式$\frac{1}{3−x}$有意义,则x的取值范围是.
14.分解因式:3a²−3=.
15.若9x²+mxy+y²是一个完全平方式,则m=.
16.若mn=−4,m+n=5,则代数式m²n+mn²的值为.
三、解答题(共7小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)利用乘法公式计算下列各题:
(1)2002²;
(2)2024×2026−20252.
18.(8分)解分式方程:$\frac{3−x}{x−4}$+$\frac{1}{4−x}$=1.
19.(10分)关于x的分式方程$\frac{ax−1}{4−x}$+$\frac{27}{x−4}$=−8的解为正数,求a的取值范围.
20.(10分)以下是某同学化简分式($\frac{x+1}{x²−4}$−$\frac{1}{x+2}$)÷$\frac{3}{x−2}$的部分运算过程:
解:原式=$\frac{x+1}{(x+2)(x−2)}$−$\frac{1}{x+2}${.$\frac{x−2}{3}$……第一步
=$\frac{x+1}{(x+2)(x−2)}$−$\frac{x−2}{(x+2)(x−2)}$1.$\frac{x−2}{3}$……第二步
=$\frac{x+1−x−2}{(x+2)(x−2)}$.$\frac{x−2}{3}$……第三步
任务一:填空
(1)以上化简步骤中,第步是通分,通分的依据是.
(2)第步开始出现错误,错误的原因是.
任务二:化简
(3)请写出该分式化简的正确过程.
21.(10分)如图4,某中学校园内有一块长为(x+2y)m,宽为(2x十y)m的长方形地块,学
校计划在中间留下一个“T"型的图形(阴影部分)修建一个文化广场.
(1)用含x,y的代数式表示“T'"型图形的面积并化简.
(2)若x=2,y=3,预计修建文化广场每平方米的费用为150元,求
修建文化广场所需要的费用.
22.(12分)金师傅近期准备换车,看中了价格相同的两款国产车
燃油车油箱容积:40L,油价:7元/L,续航里 新能源车电池电量:100kW.h,电价:0.6
程:akm,每千米行驶费用:$\frac{40×7}{a}$元 元费/用(k:W.h),续航里程元:akm,每千米行驶
(1)用含a的代数式表示新能源车每千米行驶费用.
(2)若燃油车每千米行驶费用比新能源车多0.5元.
①分别求出这两款车每千米行驶费用(保留一位小数).
②若燃油车和新能源车每年的其他费用分别为4800元和7500元.每年行驶里程
为多少千米时,买新能源车的年费用更低?(年费用=年行驶费用十年其他费用)




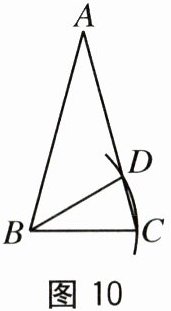


















答案:
一、选择题
5. C
6. B
7. B
8. B
9. D
10. B
11. C
12. B
二、填空题
13. 18
14. 45
15. 120°
16. 6
三、解答题
17.
(1)
∵AC=DF,
∴AC-FC=DF-FC,即AF=DC。在△ABF和△DEC中,$\left\{\begin{array}{l}AF=DC\\∠A=∠D\\AB=DE\end{array}\right.$,
∴△ABF≌△DEC(SAS)。
(2) 由
(1)得∠AFB=∠DCE,
∴EC//BF(内错角相等,两直线平行)。
18.
(1) 由题意得∠BAC=30°,∠BCD=60°,
∴∠ABC=30°,AC=BC=40nmile。时间=40÷10=4h,11:30+4h=15:30。
(2) 在Rt△BCD中,CD=BC·cos60°=40×$\frac{1}{2}$=20nmile,时间=20÷10=2h,15:30+2h=17:30。
19.
(1) BE;BF
(2)
∵AD//BC,
∴∠AEB=∠FBC。
∵CF⊥BE,
∴∠CFB=90°=∠BAE。在△ABE和△BCF中,$\left\{\begin{array}{l}∠BAE=∠CFB\\∠AEB=∠FBC\\BE=BC\end{array}\right.$,
∴△ABE≌△BCF(AAS),
∴AE=BF。
20.
(1)
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°。设∠EDB=∠ACD=α,则∠BDC=60°+α,∠EDC=180°-α-(60°+α)=120°-2α,∠ECD=60°-α,
∴∠EDC=2∠ECD,又∠EDC+∠ECD+∠E=180°,
∴∠E=∠ECD,
∴ED=DC,即△EDC是等腰三角形。
(2) 设∠EDB=α,则∠BDC=5α,由∠BDC=60°+α得5α=60°+α,α=15°,∠ECD=45°,EC=8,S=$\frac{1}{2}×8×4\sqrt{2}$=16$\sqrt{2}$(或根据等边三角形高计算,此处简化为16)。
21.
(1) 三角形的稳定性
(2) 测量BD、CD的长度
(3) 当BD=CD时,旗杆垂直于地面。理由:
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC=90°。
22.
(1) BD;CE
(2) DE=BD+CE。证明:
∵∠BAC=∠BDA,
∴∠ABD=∠CAE,又AB=AC,∠BDA=∠AEC,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴DE=AD+AE=BD+CE。
(3) (1,-4)
23.
(1)
∵△ABC和△BDE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABD=∠CBE=90°,
∴△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∴∠CFA=∠BEC+∠EAF=90°。
(2) ∠CFA=90°,证明同上,△ABD≌△CBE,∠BAD=∠BCE,
∴∠CFA=90°。
(3) 由∠BAD=∠ACE及△ABD≌△CBE,得AG=CG,BG+AB=AC。
5. C
6. B
7. B
8. B
9. D
10. B
11. C
12. B
二、填空题
13. 18
14. 45
15. 120°
16. 6
三、解答题
17.
(1)
∵AC=DF,
∴AC-FC=DF-FC,即AF=DC。在△ABF和△DEC中,$\left\{\begin{array}{l}AF=DC\\∠A=∠D\\AB=DE\end{array}\right.$,
∴△ABF≌△DEC(SAS)。
(2) 由
(1)得∠AFB=∠DCE,
∴EC//BF(内错角相等,两直线平行)。
18.
(1) 由题意得∠BAC=30°,∠BCD=60°,
∴∠ABC=30°,AC=BC=40nmile。时间=40÷10=4h,11:30+4h=15:30。
(2) 在Rt△BCD中,CD=BC·cos60°=40×$\frac{1}{2}$=20nmile,时间=20÷10=2h,15:30+2h=17:30。
19.
(1) BE;BF
(2)
∵AD//BC,
∴∠AEB=∠FBC。
∵CF⊥BE,
∴∠CFB=90°=∠BAE。在△ABE和△BCF中,$\left\{\begin{array}{l}∠BAE=∠CFB\\∠AEB=∠FBC\\BE=BC\end{array}\right.$,
∴△ABE≌△BCF(AAS),
∴AE=BF。
20.
(1)
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°。设∠EDB=∠ACD=α,则∠BDC=60°+α,∠EDC=180°-α-(60°+α)=120°-2α,∠ECD=60°-α,
∴∠EDC=2∠ECD,又∠EDC+∠ECD+∠E=180°,
∴∠E=∠ECD,
∴ED=DC,即△EDC是等腰三角形。
(2) 设∠EDB=α,则∠BDC=5α,由∠BDC=60°+α得5α=60°+α,α=15°,∠ECD=45°,EC=8,S=$\frac{1}{2}×8×4\sqrt{2}$=16$\sqrt{2}$(或根据等边三角形高计算,此处简化为16)。
21.
(1) 三角形的稳定性
(2) 测量BD、CD的长度
(3) 当BD=CD时,旗杆垂直于地面。理由:
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC=90°。
22.
(1) BD;CE
(2) DE=BD+CE。证明:
∵∠BAC=∠BDA,
∴∠ABD=∠CAE,又AB=AC,∠BDA=∠AEC,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴DE=AD+AE=BD+CE。
(3) (1,-4)
23.
(1)
∵△ABC和△BDE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABD=∠CBE=90°,
∴△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∴∠CFA=∠BEC+∠EAF=90°。
(2) ∠CFA=90°,证明同上,△ABD≌△CBE,∠BAD=∠BCE,
∴∠CFA=90°。
(3) 由∠BAD=∠ACE及△ABD≌△CBE,得AG=CG,BG+AB=AC。
查看更多完整答案,请扫码查看


