《2025年自主学习能力测评单元测试八年级数学上册人教版A版》

16. 如图15,已知AB=20m,MA⊥AB于点A,MA=10m,射线BD⊥AB于点B,点P从点B向点A运动,每秒走2m,点Q从点B出发沿BD运动,每秒走3m,P,Q两点同时从点B出发,则出发4s后,在线段MA上有一点C,使△CAP与△PBQ全等.

答案： 16.4

17. (8分)如图16,∠1=∠2,∠B=∠D,求证△ABC≌△CDA.

答案： 17.在△ABC和△CDA中，$\begin{cases} \angle B = \angle D, \\ \angle 1 = \angle 2, \\ AC = CA, \end{cases}$
∴△ABC≌△CDA(AAS)

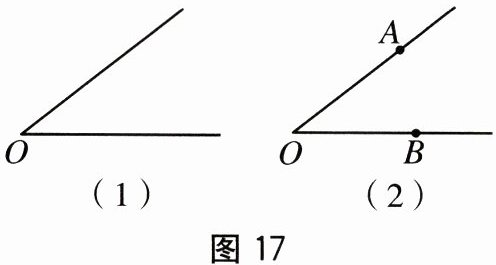
18. (10分)如图17(1)(2),下面是小明同学设计的“作一个角等于已知角”的尺规作图过程.
已知:∠O,如图17(1).
求作:一个角,使它等于∠O.
作法:如图17(2).
①在∠O的两边上分别任取一点A,B.
②以点A为圆心,OA长为半径画弧;以点B为圆心,OB长为半径画弧;两弧交于点C.
③连接AC,BC.所以,∠C即为所求作的角.
请根据小明设计的尺规作图过程,回答下列问题。
(1)使用直尺和圆规,补全图形.(保留作图痕迹,标注字母)
(2)完成以下的证明.
证明:连接AB,
∵OA=AC,AB=AB,OB=CB,
∴△OAB≌△CAB(SSS)(填“SAS”或“SSS”).
∴∠O=∠C.

答案：
18.
(1)补全的图形如答图4所示　
(2)AB,AB,CB,SSS

19. (10分)如图18,AD,BC相交于点O,BC=AD,∠C=∠D=90°.
(1)求证:AC=BD.
(2)若∠ABC=35°,求∠CAO的度数.

答案： 19.
(1)
∵∠C = ∠D = 90°,
∴△ACB和△BDA是直角三角形. 在Rt△ACB和Rt△BDA中，$\begin{cases} AB = BA, \\ BC = AD, \end{cases}$
∴Rt△ACB≌Rt△BDA(HL),
∴AC = BD　　
(2)
∵Rt△ACB≌Rt△BDA,
∴∠ABC = ∠BAD = 35°.
∵∠BAC = 90°-∠ABC = 55°,
∴∠CAO = ∠BAC -∠BAD = 20°

20. (10分)在如图19的平面直角坐标系中,画图并回答问题:

(1)画△ABC,其中A(-3,1),B(2,4),C(0,1).
(2)若点D满足AD//x轴,BD//y轴,求点D的坐标.
(3)若△ABC与△AEC全等,请画出△AEC,并写出点E的坐标(写出一种情况即可).

答案：
20.
(1)如答图5，△ABC为所求
(2)D(2,1)　　
(3)E(-5,-2)或E(2,-2)或E(-5,4)