2025年自主学习能力测评单元测试八年级数学上册人教版A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年自主学习能力测评单元测试八年级数学上册人教版A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
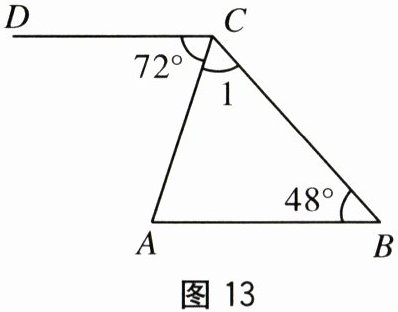
17. (8 分)如图 13,∠B = 48°,∠1 + 12° = ∠A,∠ACD = 72°,求证 AB//CD.

答案:
17.在△ABC中,∠A+∠B+∠1=180°,
∵∠B=48°,
∴∠A+∠1=132°.又
∵∠1+12°=∠A,
∴∠1+12°+∠1=132°,解得∠1=60°.
∴∠A=72°,
∴∠A=∠ACD=72°,
∴AB//CD
∵∠B=48°,
∴∠A+∠1=132°.又
∵∠1+12°=∠A,
∴∠1+12°+∠1=132°,解得∠1=60°.
∴∠A=72°,
∴∠A=∠ACD=72°,
∴AB//CD
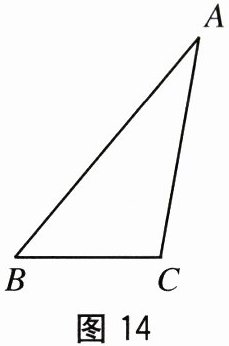
18. (10 分)如图 14,在△ABC 中,∠A = 30°,∠B = 50°.
(1)按要求画图,画 BC 边上的高 AD,∠ACB 的平分线 CE,延长 AD,EC 交于点 O.
(2)求∠AOE 的度数.
(1)按要求画图,画 BC 边上的高 AD,∠ACB 的平分线 CE,延长 AD,EC 交于点 O.
(2)求∠AOE 的度数.

答案:
18.
(1)如答图1所示,AD,CE为所求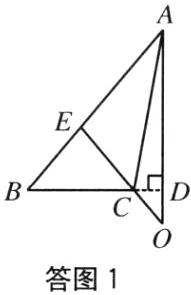
(2)
∵∠BAC=30°,∠B=50°,
∴∠ACB=180°−∠BAC−∠B =100°.
∵CE平分∠ACB,
∴∠BCE =$\frac{1}{2}$∠ACB=50°,
∴∠OCD =∠BCE =50°.
∵AD为△ABC的高,
∴∠ODC =90°,
∴∠AOE=90°−∠OCD=40°
18.
(1)如答图1所示,AD,CE为所求

(2)
∵∠BAC=30°,∠B=50°,
∴∠ACB=180°−∠BAC−∠B =100°.
∵CE平分∠ACB,
∴∠BCE =$\frac{1}{2}$∠ACB=50°,
∴∠OCD =∠BCE =50°.
∵AD为△ABC的高,
∴∠ODC =90°,
∴∠AOE=90°−∠OCD=40°
19. (10 分)用一条长为 20 cm 的细绳围成一个等腰三角形.
(1)如果腰长是底边长的 2 倍,那么各边的长是多少?
(2)能围成有一边的长是 5 cm 的等腰三角形吗? 为什么?
(1)如果腰长是底边长的 2 倍,那么各边的长是多少?
(2)能围成有一边的长是 5 cm 的等腰三角形吗? 为什么?
答案:
19.
(1)设底边长为x cm,则腰长为2x cm,由题意得x+2x+2x =20,解得x=4,
∴2x=8.三边长分别为4cm,8cm,8cm
(2)①当5cm长的边为底边时,设腰长为x cm,则5+2x=20,解得x=7.5 ②当5cm长的边为腰时,设底边长为x cm,则2×5+x=20,解得x=10.
∵5+5=10,不符合三角形两边的和大于第三边,
∴不能围成腰长是5cm的等腰三角形.综上所述,可以围成底边长是5cm的等腰三角形
(1)设底边长为x cm,则腰长为2x cm,由题意得x+2x+2x =20,解得x=4,
∴2x=8.三边长分别为4cm,8cm,8cm
(2)①当5cm长的边为底边时,设腰长为x cm,则5+2x=20,解得x=7.5 ②当5cm长的边为腰时,设底边长为x cm,则2×5+x=20,解得x=10.
∵5+5=10,不符合三角形两边的和大于第三边,
∴不能围成腰长是5cm的等腰三角形.综上所述,可以围成底边长是5cm的等腰三角形
20. (10 分)如图 15,AD 是△ABC 的角平分线,∠B = 45°,点 E 在 BC 延长线上,且 EH⊥AD 于点 H.
(1)若∠BAD = 30°,求∠ACE 的度数.
(2)若∠ACB = 85°,求∠E 的度数.
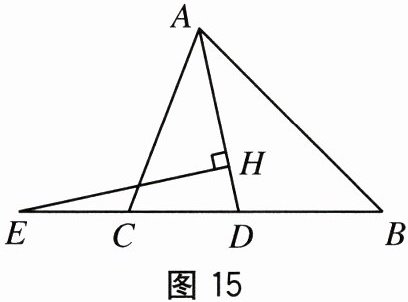
(1)若∠BAD = 30°,求∠ACE 的度数.
(2)若∠ACB = 85°,求∠E 的度数.

答案:
20.
(1)
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=30°,
∴∠BAC=60°.
∵∠ACE是△ABC的外角,
∴∠ACE=∠B+∠BAC=45°+60°=105°
(2)在△ABC中,∠CAB=180°−∠B−∠ACB=180°−45°−85°=50°,
∴∠DAB=$\frac{1}{2}$∠CAB=25°.
∵∠ADC是△ABD的外角,
∴∠ADC=∠DAB+∠B=25°+45°=70°.
∵EH ⊥AD,
∴∠E+∠ADC=90°,
∴∠E=90°−70°=20°
(1)
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=30°,
∴∠BAC=60°.
∵∠ACE是△ABC的外角,
∴∠ACE=∠B+∠BAC=45°+60°=105°
(2)在△ABC中,∠CAB=180°−∠B−∠ACB=180°−45°−85°=50°,
∴∠DAB=$\frac{1}{2}$∠CAB=25°.
∵∠ADC是△ABD的外角,
∴∠ADC=∠DAB+∠B=25°+45°=70°.
∵EH ⊥AD,
∴∠E+∠ADC=90°,
∴∠E=90°−70°=20°
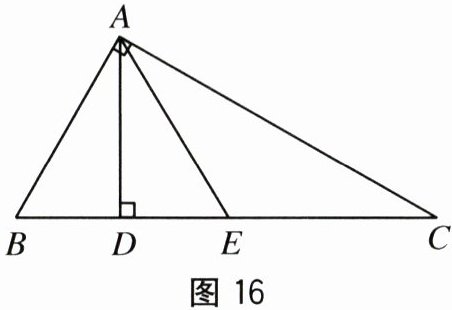
21. (10 分)如图 16 所示,已知 AD,AE 分别是△ABC 的高和中线,AB = 6 cm,AC = 8 cm,BC = 10 cm,∠CAB = 90°. 试求:
(1)AD 的长.
(2)△ABE 的面积.
(1)AD 的长.
(2)△ABE 的面积.

答案:
21.
(1)
∵∠BAC=90°,AD是边BC上的高,
∴$\frac{1}{2}$AB·AC=$\frac{1}{2}$BC·AD,
∴AD=$\frac{AB·AC}{BC}$=$\frac{6×8}{10}$=4.8(cm).
∴AD的长为4.8cm
(2)如答图2,
∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴$S_{\triangle ABC}$=$\frac{1}{2}$AB·AC=$\frac{1}{2}$×6×8=24(cm²).又
∵AE是边BC的中线,
∴BE=EC,
∴$\frac{1}{2}$BE·AD=$\frac{1}{2}$EC·AD,即$S_{\triangle ABE}$=$S_{\triangle AEC}$,
∴$S_{\triangle ABE}$=$\frac{1}{2}S_{\triangle ABC}$=12(cm²).
∴△ABE的面积是12cm²
21.
(1)
∵∠BAC=90°,AD是边BC上的高,
∴$\frac{1}{2}$AB·AC=$\frac{1}{2}$BC·AD,
∴AD=$\frac{AB·AC}{BC}$=$\frac{6×8}{10}$=4.8(cm).
∴AD的长为4.8cm
(2)如答图2,
∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴$S_{\triangle ABC}$=$\frac{1}{2}$AB·AC=$\frac{1}{2}$×6×8=24(cm²).又
∵AE是边BC的中线,
∴BE=EC,
∴$\frac{1}{2}$BE·AD=$\frac{1}{2}$EC·AD,即$S_{\triangle ABE}$=$S_{\triangle AEC}$,
∴$S_{\triangle ABE}$=$\frac{1}{2}S_{\triangle ABC}$=12(cm²).
∴△ABE的面积是12cm²

查看更多完整答案,请扫码查看


