2025年自主学习能力测评单元测试八年级数学上册人教版A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年自主学习能力测评单元测试八年级数学上册人教版A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
22. (12 分)如图 17,将三角尺(△MPN,∠MPN = 90°)放置在△ABC 上(点 P 在△ABC 内),三角尺的两边 PM,PN 恰好经过点 B 和点 C,我们来探究∠ABP 与∠ACP 是否存在某种数量关系.
【特例探究】(1)若∠A = 50°,则∠PBC + ∠PCB =
【类比探究】(2)探究∠ABP + ∠ACP 与∠A 之间的数量关系.
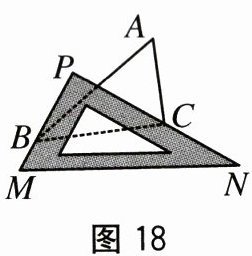
【变式探究】(3)如图 18,改变三角尺的位置,使点 P 在△ABC 外,三角尺的两边 PM,PN 仍恰好经过点 B 和点 C,探究∠ABP,∠ACP 与∠A 之间的数量关系.
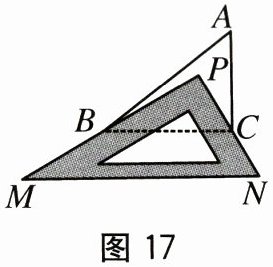
【特例探究】(1)若∠A = 50°,则∠PBC + ∠PCB =
90°
,∠ABP + ∠ACP = 40°
.【类比探究】(2)探究∠ABP + ∠ACP 与∠A 之间的数量关系.
【变式探究】(3)如图 18,改变三角尺的位置,使点 P 在△ABC 外,三角尺的两边 PM,PN 仍恰好经过点 B 和点 C,探究∠ABP,∠ACP 与∠A 之间的数量关系.


答案:
22.
(1)90° 40°
(2)在△PBC中,∠PBC+∠PCB=180°−∠BPC=180°−90°=90°.在△ABC中,∠ABP+∠ACP=180°−∠A−(∠PBC+∠PCB)=90°−∠A.
∴∠ABP+∠ACP+∠A=90°
(3)在△PBC中,∠PBC+∠PCB+∠BPC=180° ①.在△ABC中,∠ABC+∠ACB+∠A=180° ②.①−②,得∠PBC−∠ABC+∠PCB−∠ACB+∠BPC−∠A=0°,
∴∠ACP+∠A−∠ABP=90°
(1)90° 40°
(2)在△PBC中,∠PBC+∠PCB=180°−∠BPC=180°−90°=90°.在△ABC中,∠ABP+∠ACP=180°−∠A−(∠PBC+∠PCB)=90°−∠A.
∴∠ABP+∠ACP+∠A=90°
(3)在△PBC中,∠PBC+∠PCB+∠BPC=180° ①.在△ABC中,∠ABC+∠ACB+∠A=180° ②.①−②,得∠PBC−∠ABC+∠PCB−∠ACB+∠BPC−∠A=0°,
∴∠ACP+∠A−∠ABP=90°
23. (12 分)【数学经验】三角形的中线、角平分线、高是三角形的重要线段. 三角形的 3 条高所在直线交于同一点. 三角形的中线将三角形分成面积相等的两部分. 如果两个三角形的高相同,则它们的面积比等于对应底边的比,如图 19,M 是 BC 上一点,则有 $\frac{△ABM 的面积}{△ACM 的面积} = \frac{BM}{CM}$.
【初步应用】(1)如图 20,在△ABC 中,∠A = 90°,则△ABC 的三条高所在的直线交于点
【综合应用】(2)如图 21,在△ABC 中,∠ACB > ∠B,AD 平分∠BAC,过点 C 作 CE⊥AD 于点 E.
①若∠ACB = 80°,∠B = 30°,则∠ECD =
②请写出∠ECD 与∠ACB,∠B 之间的数量关系,并说明理由.
【拓展延伸】(3)如图 22,在△ABC 中,M 是 BC 上一点,且 BM = $\frac{1}{4}$BC,N 是 AC 的中点. 若△ABC 的面积是 m,请直接写出四边形 CMDN 的面积(用含 m 的代数式表示).

【初步应用】(1)如图 20,在△ABC 中,∠A = 90°,则△ABC 的三条高所在的直线交于点
A
.【综合应用】(2)如图 21,在△ABC 中,∠ACB > ∠B,AD 平分∠BAC,过点 C 作 CE⊥AD 于点 E.
①若∠ACB = 80°,∠B = 30°,则∠ECD =
25
°.②请写出∠ECD 与∠ACB,∠B 之间的数量关系,并说明理由.
【拓展延伸】(3)如图 22,在△ABC 中,M 是 BC 上一点,且 BM = $\frac{1}{4}$BC,N 是 AC 的中点. 若△ABC 的面积是 m,请直接写出四边形 CMDN 的面积(用含 m 的代数式表示).

答案:
23.
(1)A
(2)①25 ②2∠ECD=∠ACB−∠B.理由如下:
∵CE⊥AD,
∴∠AEC=90°,
∴∠ACE=90°−∠CAD,
∴∠ECD=∠ACB−∠ACE=∠ACB+∠CAD−90°.
∵AD平分∠BAC,
∴∠CAD=∠BAD=$\frac{1}{2}$∠BAC.
∵∠BAC=180°−∠B−∠ACB,
∴∠CAD=90°−$\frac{1}{2}$∠B−$\frac{1}{2}$∠ACB,
∴∠ECD=∠ACB+∠CAD−90°=∠ACB+90°−$\frac{1}{2}$∠B−$\frac{1}{2}$∠ACB−90°=$\frac{1}{2}$∠ACB−$\frac{1}{2}$∠B,
∴2∠ECD=∠ACB−∠B
(3)$\frac{9}{20}$m.连接CD,如答图3所示,
∵N是AC的中点,
∴$\frac{S_{\triangle ADN}}{S_{\triangle CDN}}$=$\frac{AN}{CN}$=1,
∴$S_{\triangle ADN}$=$S_{\triangle CDN}$.同理$S_{\triangle ABN}$=$S_{\triangle CBN}$.设$S_{\triangle ADN}$=$S_{\triangle CDN}$=a,
∵△ABC的面积是m,
∴$S_{\triangle ABN}$=$S_{\triangle CBN}$=$\frac{1}{2}m$,
∴$S_{\triangle BCD}$=$S_{\triangle BAD}$=$\frac{1}{2}m$ -a.
∵BM=$\frac{1}{4}$BC,
∴$\frac{BM}{CM}$=$\frac{1}{3}$,
∴$\frac{S_{\triangle BDM}}{S_{\triangle CDM}}$=$\frac{BM}{CM}$=$\frac{1}{3}$,$\frac{S_{\triangle ABM}}{S_{\triangle ACM}}$=$\frac{BM}{CM}$=$\frac{1}{3}$,
∴$S_{\triangle CDM}$=3$S_{\triangle BDM}$,$S_{\triangle ACM}$=3$S_{\triangle ABM}$,
∴$S_{\triangle CDM}$=$\frac{3}{4}S_{\triangle BCD}$=$\frac{3}{4}$×($\frac{1}{2}m$ -a)=$\frac{3}{8}m$ -$\frac{3}{4}a$,$S_{\triangle ACM}$=$\frac{3}{4}S_{\triangle ABC}$=$\frac{3}{4}m$.
∵$S_{\triangle ACM}$=$S_{四边形CMDN}$+$S_{\triangle ADN}$=$S_{\triangle CDM}$+$S_{\triangle CDN}$+$S_{\triangle ADN}$,即$\frac{3}{4}m$ =$\frac{3}{8}m$ -$\frac{3}{4}a$+a+a,解得a=$\frac{3}{10}m$,
∴$S_{四边形CMDN}$=$S_{\triangle CDM}$+$S_{\triangle CDN}$=$\frac{3}{8}m$ -$\frac{3}{4}$×$\frac{3}{10}m$+$\frac{3}{10}m$=$\frac{9}{20}m$
23.
(1)A
(2)①25 ②2∠ECD=∠ACB−∠B.理由如下:
∵CE⊥AD,
∴∠AEC=90°,
∴∠ACE=90°−∠CAD,
∴∠ECD=∠ACB−∠ACE=∠ACB+∠CAD−90°.
∵AD平分∠BAC,
∴∠CAD=∠BAD=$\frac{1}{2}$∠BAC.
∵∠BAC=180°−∠B−∠ACB,
∴∠CAD=90°−$\frac{1}{2}$∠B−$\frac{1}{2}$∠ACB,
∴∠ECD=∠ACB+∠CAD−90°=∠ACB+90°−$\frac{1}{2}$∠B−$\frac{1}{2}$∠ACB−90°=$\frac{1}{2}$∠ACB−$\frac{1}{2}$∠B,
∴2∠ECD=∠ACB−∠B
(3)$\frac{9}{20}$m.连接CD,如答图3所示,
∵N是AC的中点,
∴$\frac{S_{\triangle ADN}}{S_{\triangle CDN}}$=$\frac{AN}{CN}$=1,
∴$S_{\triangle ADN}$=$S_{\triangle CDN}$.同理$S_{\triangle ABN}$=$S_{\triangle CBN}$.设$S_{\triangle ADN}$=$S_{\triangle CDN}$=a,
∵△ABC的面积是m,
∴$S_{\triangle ABN}$=$S_{\triangle CBN}$=$\frac{1}{2}m$,
∴$S_{\triangle BCD}$=$S_{\triangle BAD}$=$\frac{1}{2}m$ -a.
∵BM=$\frac{1}{4}$BC,
∴$\frac{BM}{CM}$=$\frac{1}{3}$,
∴$\frac{S_{\triangle BDM}}{S_{\triangle CDM}}$=$\frac{BM}{CM}$=$\frac{1}{3}$,$\frac{S_{\triangle ABM}}{S_{\triangle ACM}}$=$\frac{BM}{CM}$=$\frac{1}{3}$,
∴$S_{\triangle CDM}$=3$S_{\triangle BDM}$,$S_{\triangle ACM}$=3$S_{\triangle ABM}$,
∴$S_{\triangle CDM}$=$\frac{3}{4}S_{\triangle BCD}$=$\frac{3}{4}$×($\frac{1}{2}m$ -a)=$\frac{3}{8}m$ -$\frac{3}{4}a$,$S_{\triangle ACM}$=$\frac{3}{4}S_{\triangle ABC}$=$\frac{3}{4}m$.
∵$S_{\triangle ACM}$=$S_{四边形CMDN}$+$S_{\triangle ADN}$=$S_{\triangle CDM}$+$S_{\triangle CDN}$+$S_{\triangle ADN}$,即$\frac{3}{4}m$ =$\frac{3}{8}m$ -$\frac{3}{4}a$+a+a,解得a=$\frac{3}{10}m$,
∴$S_{四边形CMDN}$=$S_{\triangle CDM}$+$S_{\triangle CDN}$=$\frac{3}{8}m$ -$\frac{3}{4}$×$\frac{3}{10}m$+$\frac{3}{10}m$=$\frac{9}{20}m$

查看更多完整答案,请扫码查看


