《2025年同步练习册河北教育出版社七年级数学上册冀教版》

5. 为了备战足球联赛，一名足球守门员练习往返跑，从守门位置出发，向前记作正数，返回记作负数. 数据（单位：$m$）记录如下：
$+6$，$-5$，$-4$，$+10$，$+4$，$-3$，$-6$.
(1)通过计算说明守门员最后是否回到守门位置.
(2)在练习的过程中，守门员离开守门位置最远是多少米？

答案：
(1)守门员最后没有回到守门位置
(2)11 m

6. 如图，阶梯的每个台阶上都标着一个有理数. 若任意相邻三个台阶上的数之和都相等，则前$19$个台阶上所标有理数之和是多少？

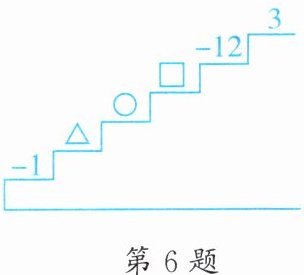
答案： 1. 首先，根据“任意相邻三个台阶上的数之和都相等”列等式：
设$\triangle =a$，$◯ =b$，$□ =c$。
由$-1 + a + b=a + b + c$，可得$c=-1$；
又因为$a + b + c=b + c-12$，把$c = - 1$代入，即$a-1=b - 1-12$，再由$b + c-12=c-12 + 3$，把$c=-1$代入得$b-1-12=-1 - 12 + 3$，解得$b = 3$；
把$b = 3$，$c=-1$代入$-1 + a + b=a + b + c$，$-1+a + 3=a + 3-1$（恒成立），再根据$a + b + c=b + c-12$，$a+3 - 1=3 - 1-12$，解得$a=-12$。
所以这组数据是以$-1$，$-12$，$3$依次循环出现的。
2. 然后，计算循环周期：
因为$19÷3 = 6\cdots\cdots1$。
一个周期$(-1-12 + 3)$的和为$-1-12 + 3=-10$。
3. 最后，计算前$19$个台阶上数的和：
前$19$个数的和$S=6×(-10)+(-1)$。
根据有理数乘法和加法法则，$S=-60 - 1=-61$。
答：前$19$个台阶上所标有理数之和是$-61$。

7. 某水库在星期一的水位是$110.3m$，星期二水位下降了$0.2m$，星期三水位上升了$0.7m$，星期四水位下降了$0.8m$.
(1)规定水位上升为正、下降为负，请将每天水位变化的情况用正数或负数表示出来.
(2)星期四的水位是多少米？

答案： 解：
(1)每天水位的变化情况表示如下：星期二为-0.2 m，星期三为+0.7 m，星期四为-0.8 m.
(2)根据题意，得110.3+(-0.2)+(+0.7)+(-0.8)=[110.3+(+0.7)]+[(-0.2)+(-0.8)]=111+(-1)=110(m).答：所以星期四的水位是110 m.