*7. 任意一个等腰直角三角形都可以分割成四个小三角形,使每个小三角形都与原等腰直角三角形相似(如图①是其中的一种分法)。你还有几种不同的分割方案?请在备用三角形(图②③④)中画出分割图形。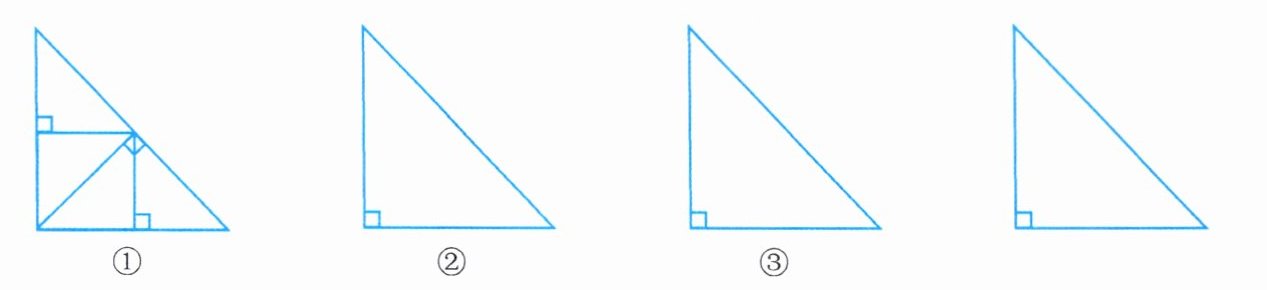

答案:
如图
如图

1. 可以判定$\triangle ABC \sim \triangle A'B'C'$的条件是(
A.$\angle A = \angle A'$.
B.$\frac{AB}{A'B'} = \frac{AC}{A'C'}$,且$\angle C = \angle C'$.
C.$\frac{AB}{A'B'} = \frac{AC}{A'C'} = \frac{BC}{B'C'}$.
D.$\frac{AB}{A'B'} = \frac{AC}{A'C'}$,且$\angle B = \angle B'$.
C
)A.$\angle A = \angle A'$.
B.$\frac{AB}{A'B'} = \frac{AC}{A'C'}$,且$\angle C = \angle C'$.
C.$\frac{AB}{A'B'} = \frac{AC}{A'C'} = \frac{BC}{B'C'}$.
D.$\frac{AB}{A'B'} = \frac{AC}{A'C'}$,且$\angle B = \angle B'$.
答案:
C
2. 已知一个三角形三边的长分别为6 cm,9 cm,7.5 cm,另一个三角形三边的长分别为8 cm,10 cm,12 cm. 试判断这两个三角形是否相似,并说明理由.
答案:
相似.理由:$\frac{7.5}{10}=\frac{9}{12}=\frac{6}{8}$
查看更多完整答案,请扫码查看


