《2025年作业本浙江教育出版社九年级数学上册浙教版》

1. 如图,在$\odot O$中,$\widehat{AB}= \widehat{CD}$.有下列结论:
①$AB= CD$;②$AC= BD$;③$\angle AOC= \angle BOD$;④$\widehat{AC}= \widehat{BD}$.
其中正确的有(B)

A.②③④.
B.①②③④.
C.①②④.
D.①②③.

答案： B

2. 已知:如图,在$\odot O$中,弦$AD= BC$,连结$AB$,$CD$.求证:$AB= CD$.

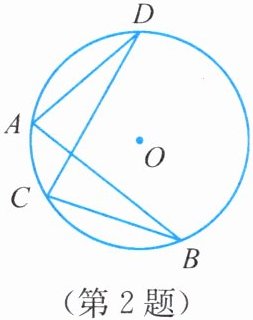
答案： 证$\widehat{AB}=\widehat{CD}$

3. 如图,$\triangle ABC内接于\odot O$,连结$OA$,$OC$.已知$AB= AC$,$\widehat{BC}的度数为100^\circ$,求$\angle AOC和\widehat{AC}$的度数.

答案： $\angle AOC=130^\circ$,$\widehat{AC}=130^\circ$

4. 已知:如图,$AB$,$CD是\odot O$的弦,且$AB= CD$,$M$,$N分别是AB$,$CD$的中点.求证:$\angle AMN= \angle CNM$.

答案： 证明：连接OM，ON。
∵M，N分别是AB，CD的中点，O是圆心，
∴OM⊥AB，ON⊥CD，AM=½AB，CN=½CD。
∵AB=CD，
∴AM=CN，OM=ON。
∴∠OMN=∠ONM。
∵∠OMA=∠ONC=90°，
∴∠OMA - ∠OMN = ∠ONC - ∠ONM，
即∠AMN=∠CNM。