《2025年作业本浙江教育出版社九年级数学上册浙教版》

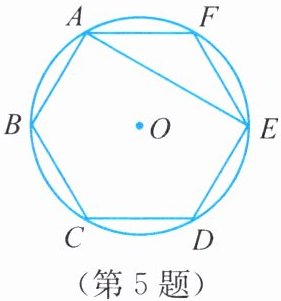
5. 如图,点$A$,$B$,$C$,$D$,$E$,$F都在\odot O$上,且$AB= BC= CD= DE= EF= AF$.若$\odot O$的半径为6,求$AE$的长.

答案： 连结AO,FO,EO,则$\angle AOF=\angle FOE=60^\circ$,则$\triangle AOF$和$\triangle FOE$均为边长为6的等边三角形,且$FO\perp AE$.可求得$AE=6\sqrt{3}$

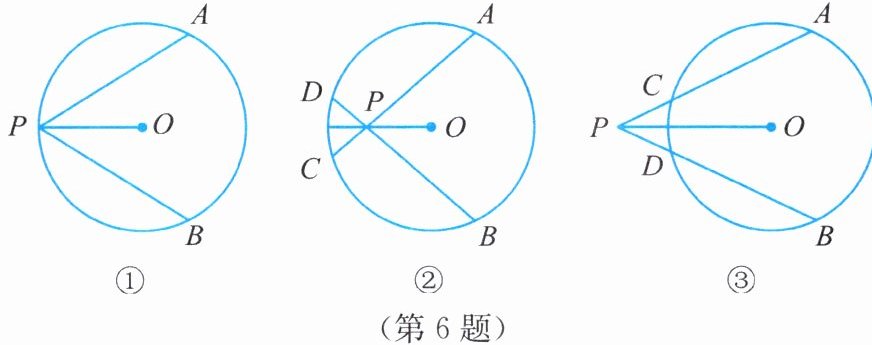
6. (1)如图①,过$\odot O上一点P作两条弦PA$,$PB$.若$PA= PB$,则$PO平分\angle APB$.为什么?
(2)如图②,若点$P在\odot O$内,过点$P的两条弦AC$,$DB$相等,则$PO平分\angle APB$吗?为什么?
(3)如图③,若点$P在\odot O$外,过点$P作PA$,$PB$,分别交$\odot O于点A$,$C和B$,$D$,且$AC= BD$,则$PO平分\angle APB$吗?为什么?

答案： $(1)$
解：过$O$分别作$OE\perp PA$于$E$，$OF\perp PB$于$F$。
因为$PA = PB$，根据在同圆或等圆中，相等的弦所对的弦心距相等，所以$OE = OF$。
又因为$OE\perp PA$，$OF\perp PB$，根据角平分线的判定定理（到角两边距离相等的点在角的平分线上），所以$PO$平分$\angle APB$。
$(2)$
解：过$O$分别作$OE\perp PA$于$E$，$OF\perp PB$于$F$。
连接$OA$，$OB$，$OC$，$OD$。
因为$AC = BD$，所以$\overset{\frown}{AC}=\overset{\frown}{BD}$（在同圆或等圆中，相等的弦所对的弧相等），则$\overset{\frown}{AC}+\overset{\frown}{CD}=\overset{\frown}{BD}+\overset{\frown}{CD}$，即$\overset{\frown}{AD}=\overset{\frown}{BC}$，所以$\angle AOD=\angle BOC$。
又因为$OA = OB$，$OD = OC$，所以$\triangle AOD\cong\triangle BOC$（$SAS$），则$OE = OF$（全等三角形对应边上的高相等）。
因为$OE\perp PA$，$OF\perp PB$，根据角平分线的判定定理，所以$PO$平分$\angle APB$。
$(3)$
解：过$O$分别作$OE\perp PA$于$E$，$OF\perp PB$于$F$。
连接$OA$，$OB$，$OC$，$OD$。
因为$AC = BD$，所以$\overset{\frown}{AC}=\overset{\frown}{BD}$（在同圆或等圆中，相等的弦所对的弧相等），则$\overset{\frown}{AC}+\overset{\frown}{AD}=\overset{\frown}{BD}+\overset{\frown}{BC}$，即$\overset{\frown}{CD}=\overset{\frown}{AB}$，所以$\angle AOB=\angle COD$。
又因为$OA = OB$，$OC = OD$，所以$\triangle AOB\cong\triangle COD$（$SAS$），则$OE = OF$（全等三角形对应边上的高相等）。
因为$OE\perp PA$，$OF\perp PB$，根据角平分线的判定定理，所以$PO$平分$\angle APB$。
综上，$(1)$、$(2)$、$(3)$中$PO$都平分$\angle APB$。