《2025年作业本浙江教育出版社九年级数学上册浙教版》

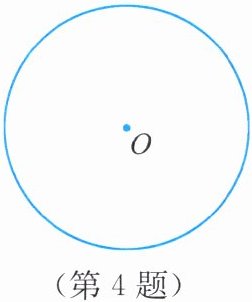
4. 如图,已知⊙O.
(1)用直尺和圆规作⊙O的内接正三角形.
(2)若⊙O的半径为4,求⊙O的内接正三角形的边长.

答案： （1）略 （2）$4\sqrt{3}$

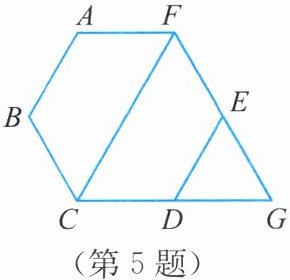
5. 已知：如图,正六边形ABCDEF的边长为6 cm,延长FE,CD,相交于点G.
(1)求证：△FCG是正三角形.
(2)求正三角形FCG的高线长.

答案： 1. （1）证明：
因为六边形$ABCDEF$是正六边形，所以$\angle AFE=\angle FED = \angle EDC=\angle DCB=\angle CBA=\angle BAF = 120^{\circ}$。
则$\angle GFE = 180^{\circ}-\angle AFE=60^{\circ}$，$\angle GDC = 180^{\circ}-\angle EDC = 60^{\circ}$。
在$\triangle FEG$中，$\angle GFE = 60^{\circ}$，$\angle FEG=\angle FED = 120^{\circ}$，所以$\angle G=180^{\circ}-\angle GFE-\angle FEG = 180^{\circ}-60^{\circ}-120^{\circ}=60^{\circ}$。
又因为正六边形$ABCDEF$的边长为$6cm$，$EF = ED = DC = 6cm$，$\angle GFE=\angle GDC = 60^{\circ}$，$\angle G = 60^{\circ}$。
所以$\triangle FCG$的三个内角都是$60^{\circ}$，所以$\triangle FCG$是正三角形。
2. （2）
已知正三角形$FCG$的边长$FG=FC = CG$，因为$EF = 6cm$，$ED = 6cm$，$DC = 6cm$，所以$FG=FC=CG=6 + 6=12cm$。
设正三角形$FCG$的高线长为$h$，根据正三角形的性质，由勾股定理$h=\sqrt{FC^{2}-\left(\frac{FC}{2}\right)^{2}}$（对于正三角形，边长为$a$，高$h=\sqrt{a^{2}-\left(\frac{a}{2}\right)^{2}}$）。
把$a = 12$代入$h=\sqrt{a^{2}-\left(\frac{a}{2}\right)^{2}}=\sqrt{12^{2}-6^{2}}=\sqrt{(12 + 6)(12 - 6)}=\sqrt{18×6}=\sqrt{108}=6\sqrt{3}(cm)$。
综上，（1）已证$\triangle FCG$是正三角形；（2）正三角形$FCG$的高线长为$6\sqrt{3}cm$。

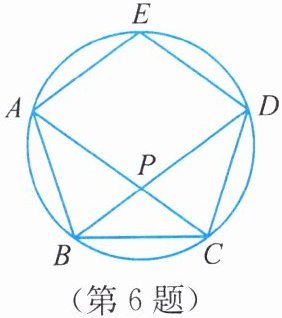
6. 已知：如图,在圆内接正五边形ABCDE中,对角线AC,BD交于点P.
(1)求∠APD的度数.
(2)求证：四边形EAPD是菱形.

答案： （1）$108°$ （2）略