9. 如图,在某场足球比赛中,球员甲从球门底部中心点$O$的正前方10 m处起脚射门,足球沿抛物线飞向球门中心线. 当足球飞离地面高度为3 m时达到最高点,此时足球飞行的水平距离为6 m. 已知球门的横梁高为2.44 m.
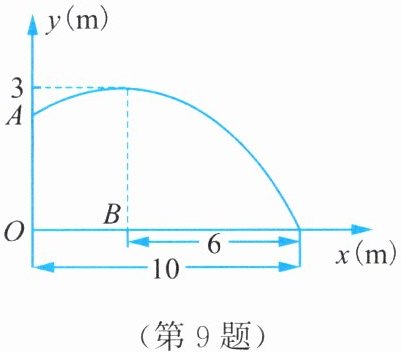
(1)建立如图所示直角坐标系. 此次射门,足球能否射进球门(不计其他影响因素)?
(2)守门员站在距离球门2 m处,他跳起时手的最大摸高为2.52 m. 问:他能阻止球员甲的此次射门吗?如果不能,他至少后退多少米才能阻止球员甲的此次射门?

(1)建立如图所示直角坐标系. 此次射门,足球能否射进球门(不计其他影响因素)?
(2)守门员站在距离球门2 m处,他跳起时手的最大摸高为2.52 m. 问:他能阻止球员甲的此次射门吗?如果不能,他至少后退多少米才能阻止球员甲的此次射门?
答案:
(1)$ y=-\frac{1}{12}(x-4)^{2}+3 $.当$ x=0 $时,$ y=\frac{5}{3}<2.44 $,所以足球能射入球门
(2)当$ x=2 $时,$ y=\frac{8}{3}>2.52 $,所以守门员不能阻止此次射门.由$ -\frac{1}{12}(x-4)^{2}+3 $
$ =2.52 $,得$ x=1.6 $.所以守门员至少后退0.4m才能阻止球员甲的此次射门
(2)当$ x=2 $时,$ y=\frac{8}{3}>2.52 $,所以守门员不能阻止此次射门.由$ -\frac{1}{12}(x-4)^{2}+3 $
$ =2.52 $,得$ x=1.6 $.所以守门员至少后退0.4m才能阻止球员甲的此次射门
10. 在直角坐标系中,$\triangle AOB$的位置如图所示,$\angle AOB= 90^\circ$,$AO= BO$,点$A的坐标为(-3,1)$.
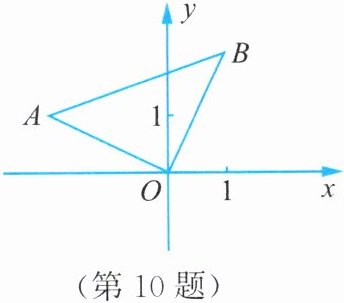
(1)求点$B$的坐标.
(2)求过点$A$,$O$,$B$的抛物线的函数表达式.
(3)在(2)的条件下,设点$B关于抛物线的对称轴l的对称点为B_1$,求$\triangle AB_1B$的面积.

(1)求点$B$的坐标.
(2)求过点$A$,$O$,$B$的抛物线的函数表达式.
(3)在(2)的条件下,设点$B关于抛物线的对称轴l的对称点为B_1$,求$\triangle AB_1B$的面积.
答案:
(1)$ B(1,3) $ (2)$ y=\frac{5}{6}x^{2}+\frac{13}{6}x $ (3)$ S_{\triangle AB_{1}B}=\frac{23}{5} $
查看更多完整答案,请扫码查看


