第9页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
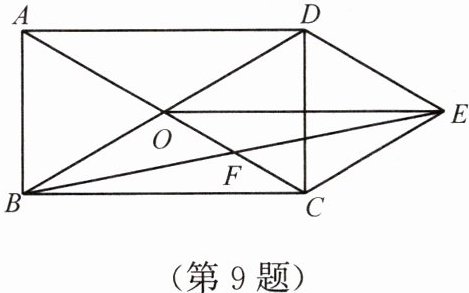
9. 如图,矩形ABCD的对角线AC,BD相交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.
(1)求证:四边形OBCE是平行四边形;
(2)连接BE交AC于点F,若AB=2,∠AOB=60°,求BF的长.
(1)求证:四边形OBCE是平行四边形;
(2)连接BE交AC于点F,若AB=2,∠AOB=60°,求BF的长.

答案:
9.
(1)证明:
∵四边形ABCD是矩形,
∴OA = OB = OC = OD.
∵四边形OCED是平行四边形,
∴四边形OCED为菱形,
∴CE//OB,CE = OB,
∴四边形OBCE是平行四边形.
(2)解:如图,过点F作FM⊥BC于点M,过点O作ON⊥BC于点N.

∵FM⊥BC,ON⊥BC,
∴ON//FM.
∵AO = OC,
∴ON = $\frac{1}{2}$AB = 1.
∵OF = FC,
∴FM = $\frac{1}{2}$ON = $\frac{1}{2}$.
∵∠AOB = 60°,OA = OB,
∴∠OAB = 60°,∠ACB = 30°.
在Rt△ABC中,
∵AB = 2,∠ACB = 30°,
∴BC = 2$\sqrt{3}$.
∵∠ACB = 30°,FM = $\frac{1}{2}$,
∴CM = $\frac{\sqrt{3}}{2}$,
∴BM = BC - CM = $\frac{3\sqrt{3}}{2}$,
∴BF = $\sqrt{BM^{2} + FM^{2}}$ = $\sqrt{7}$.
9.
(1)证明:
∵四边形ABCD是矩形,
∴OA = OB = OC = OD.
∵四边形OCED是平行四边形,
∴四边形OCED为菱形,
∴CE//OB,CE = OB,
∴四边形OBCE是平行四边形.
(2)解:如图,过点F作FM⊥BC于点M,过点O作ON⊥BC于点N.

∵FM⊥BC,ON⊥BC,
∴ON//FM.
∵AO = OC,
∴ON = $\frac{1}{2}$AB = 1.
∵OF = FC,
∴FM = $\frac{1}{2}$ON = $\frac{1}{2}$.
∵∠AOB = 60°,OA = OB,
∴∠OAB = 60°,∠ACB = 30°.
在Rt△ABC中,
∵AB = 2,∠ACB = 30°,
∴BC = 2$\sqrt{3}$.
∵∠ACB = 30°,FM = $\frac{1}{2}$,
∴CM = $\frac{\sqrt{3}}{2}$,
∴BM = BC - CM = $\frac{3\sqrt{3}}{2}$,
∴BF = $\sqrt{BM^{2} + FM^{2}}$ = $\sqrt{7}$.
10. 如图,点A,D,G,M在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a,EF=b,HN=c,则a,b,c之间的大小关系为(
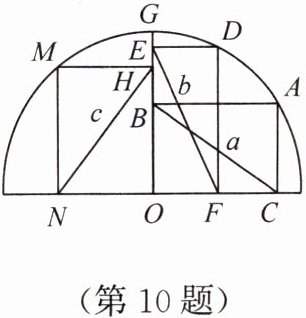
A.a>b>c
B.a<b<c
C.a=b=c
D.a>c>b
C
)。
A.a>b>c
B.a<b<c
C.a=b=c
D.a>c>b
答案:
10.C
11. 如图,在矩形ABCD中,BD=2√{5},AB在x轴上.且点A的横坐标为-1,若以点A为圆心,对角线AC的长为半径作弧,交x轴的正半轴于点M,则点M的坐标为(
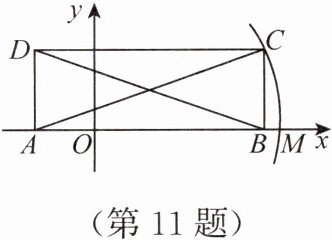
A.(2+√{5},0)
B.(2√{5}+1,0)
C.(2√{5}-1,0)
D.(2√{5},0)
C
)。
A.(2+√{5},0)
B.(2√{5}+1,0)
C.(2√{5}-1,0)
D.(2√{5},0)
答案:
11.C
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证。
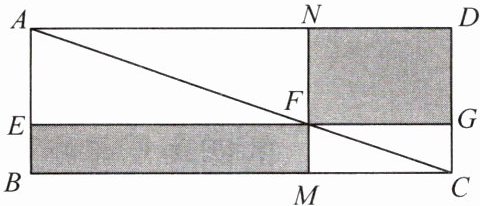
请根据该图完成这个推论的证明过程。
证明:$S_{矩形NFGD}=S_{△ADC}-(S_{△ANF}+S_{△FGC}),$
$S_{矩形EBMF}=S_{△ABC}-(_$
易知,$S_{△ADC}=S_{△ABC},$_
可得$S_{矩形NFGD}=S_{矩形EBMF}。$

请根据该图完成这个推论的证明过程。
证明:$S_{矩形NFGD}=S_{△ADC}-(S_{△ANF}+S_{△FGC}),$
$S_{矩形EBMF}=S_{△ABC}-(_$
S_{△AEF}
$+$S_{△FMC}
$_)。$易知,$S_{△ADC}=S_{△ABC},$_
$S_{△ANF}$
=$S_{△AEF}$
_,_$S_{△RGC}$
=$S_{△FMC}$
_。可得$S_{矩形NFGD}=S_{矩形EBMF}。$
答案:
课堂延伸
S△AEF S△FMC S△ANF S△AEF S△RGC S△FMC
S△AEF S△FMC S△ANF S△AEF S△RGC S△FMC
(2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是(
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠ACB=∠ACD
C
)。
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠ACB=∠ACD
答案:
中考链接
C
C
查看更多完整答案,请扫码查看


