《2025年初中同步练习册九年级数学上册北师大版北京师范大学出版社》

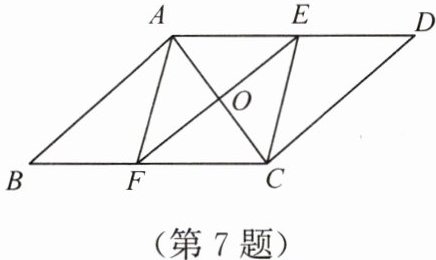
7. 如图，在 $□ ABCD$ 中，$AC \perp AB$，$O$ 为 $AC$ 的中点，经过点 $O$ 的线段交 $AD$ 于点 $E$，交 $BC$ 于点 $F$，连接 $AF$，$CE$，现在添加一个适当的条件，使四边形 $AFCE$ 是菱形，现有下列条件：① $OE = OA$；② $EF \perp AC$；③ $E$ 为 $AD$ 的中点。其中正确的个数为(C)。

A.$0$
B.$1$
C.$2$
D.$3$

答案： 7. C

阅读下列材料，完成后面的问题。如图，在 $□ ABCD$ 中，$∠BAD$ 的平分线 $AE$ 与 $BC$ 相交于点 $E$，$∠ABC$ 的平分线 $BF$ 与 $AD$ 相交于点 $F$，$AE$ 与 $BF$ 相交于点 $O$，连接 $EF$。求证：四边形 $ABEF$ 是菱形。
证明：①∵四边形 $ABCD$ 是平行四边形，
②∴$AD // BC$，
③∴$∠ABE + ∠BAF = 180^{\circ}$。
④∵$AE$，$BF$ 分别平分 $∠BAF$，$∠ABE$，
⑤∴$∠1 = ∠2 = \frac{1}{2}∠BAF$，$∠3 = ∠4 = \frac{1}{2}∠ABE$，
⑥∴$∠1 + ∠3 = \frac{1}{2}(∠BAF + ∠ABE) = 90^{\circ}$，
⑦∴$∠AOB = 90^{\circ}$，
⑧∴$AE \perp BF$，
⑨∴四边形 $ABEF$ 是菱形。
问：(1) 上述证明是否正确？答：错误。
(2) 如有错误，在第⑨步推理错误，应在第⑧步后添加如下证明过程：

答案： 解：
(1)错误
(2)⑨ ⑧
$\because AD// BC$，$\therefore \angle AEB=\angle 2$。
又$\because \angle 1=\angle 2$，$\therefore \angle AEB=\angle 1$，
$\therefore BA=BE$，同理$AB=AF$，$\therefore BE=AF$，又$AF// BE$，
$\therefore$四边形$ABEF$是平行四边形。

(2023·张家界) 如图，已知点 $A$，$D$，$C$，$B$ 在同一条直线上，且 $AD = BC$，$AE = BF$，$CE = DF$。
(1) 求证：$AE // BF$；
(2) 若 $DF = FC$，求证：四边形 $DECF$ 是菱形。

答案： 证明：
(1)$\because AD=BC$，
$\therefore AD+CD=BC+CD$，
$\therefore AC=BD$。
$\because AE=BF$，$CE=DF$，
$\therefore \triangle AEC\cong\triangle BFD(SSS)$，
$\therefore \angle A=\angle B$，
$\therefore AE// BF$。
(2)$\because \triangle AEC\cong\triangle BFD$，
$\therefore \angle ECA=\angle FDB$，
$\therefore EC// DF$。
$\because EC=DF$，
$\therefore$四边形$DECF$是平行四边形。
$\because DF=FC$，
$\therefore$四边形$DECF$是菱形。