第73页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
4. 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2 m,旗杆底部与平面镜的水平距离为16 m.若小明的眼睛与地面距离为1.5 m,则旗杆的高度为(
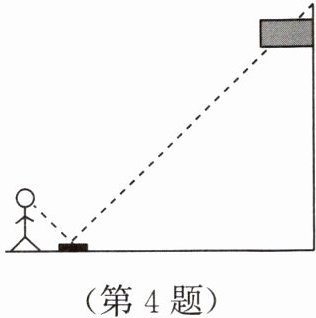
A.$\frac{16}{3}$ m
B.9 m
C.12 m
D.$\frac{64}{3}$ m
C
)。
A.$\frac{16}{3}$ m
B.9 m
C.12 m
D.$\frac{64}{3}$ m
答案:
4.C
5. 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是拿一根高3.5 m的竹竿直立在离旗杆27 m的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C,D两点的距离为3 m,小芳的目高为1.5 m,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
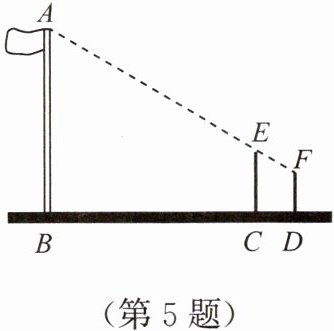

答案:
5. 解:这种测量方法可行. 理由如下:
设旗杆高$AB=x$ m,过点$F$作$FG\perp AB$于点$G$,交
$CE$于点$H$(图略).
所以$\triangle AGF\sim\triangle EHF$.
因为$FD=1.5$ m,$GF=27 + 3 = 30$(m),$HF=3$ m,
所以$EH=3.5 - 1.5 = 2$(m),$AG=(x - 1.5)$m.
由$\triangle AGF\sim\triangle EHF$,
得$\frac{AG}{EH}=\frac{GF}{HF}$,即$\frac{x - 1.5}{2}=\frac{30}{3}$,
解得$x = 21.5$.
答:旗杆的高为$21.5$ m.
设旗杆高$AB=x$ m,过点$F$作$FG\perp AB$于点$G$,交
$CE$于点$H$(图略).
所以$\triangle AGF\sim\triangle EHF$.
因为$FD=1.5$ m,$GF=27 + 3 = 30$(m),$HF=3$ m,
所以$EH=3.5 - 1.5 = 2$(m),$AG=(x - 1.5)$m.
由$\triangle AGF\sim\triangle EHF$,
得$\frac{AG}{EH}=\frac{GF}{HF}$,即$\frac{x - 1.5}{2}=\frac{30}{3}$,
解得$x = 21.5$.
答:旗杆的高为$21.5$ m.
6. 小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE与点A在同一条直线上.测得边DF离地面的高度为1.4 m,点D到AB的距离等于6 m(如图所示).已知DF=30 cm,EF=20 cm,那么树AB的高度等于(
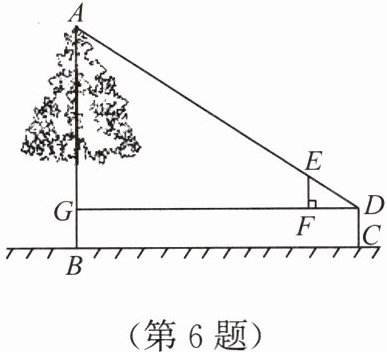
A.4 m
B.5.4 m
C.9 m
D.10.4 m
B
)。
A.4 m
B.5.4 m
C.9 m
D.10.4 m
答案:
6.B
7. 如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,张强扛着箱子(人与箱子的总高度约为2.2 m)乘电梯刚好完全通过.请你根据图中数据回答,两层楼之间的高约为(
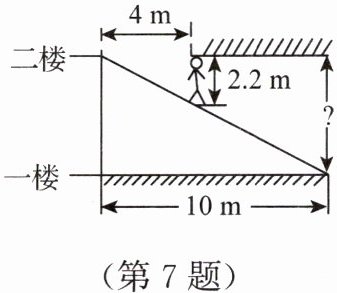
A.5.5 m
B.6.2 m
C.11 m
D.2.2 m
A
)。
A.5.5 m
B.6.2 m
C.11 m
D.2.2 m
答案:
7.A
8. 在同一时刻两根竹竿在太阳光下的影子如图所示,其中竹竿AB=2 m,它的影子BC=1.6 m,竹竿PQ的影子有一部分落在了墙上,PM=1.2 m,MN=0.8 m,则竹竿PQ的长度为
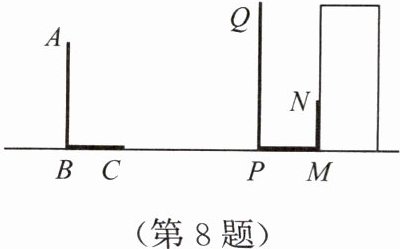
$2.3$ m
。
答案:
8.$2.3$ m
查看更多完整答案,请扫码查看


