《2025年初中同步练习册九年级数学上册北师大版北京师范大学出版社》

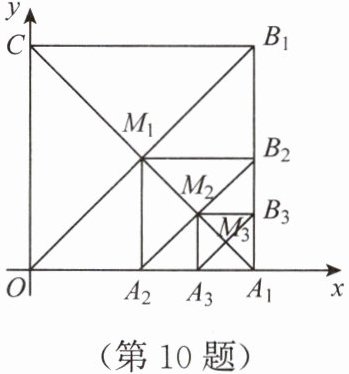
10. 如图，在平面直角坐标系中，边长为 $1$ 的正方形 $OA_1B_1C$ 的对角线 $A_1C$ 和 $OB_1$ 交于点 $M_1$；以 $M_1A_1$ 为对角线作第二个正方形 $A_2A_1B_2M_1$，对角线 $A_1M_1$ 和 $A_2B_2$ 交于点 $M_2$；以 $M_2A_1$ 为对角线作第三个正方形 $A_3A_1B_3M_2$，对角线 $A_1M_2$ 和 $A_3B_3$ 交于点 $M_3$……依此类推，这样作第 $n$ 个正方形的面积为(C)。

A.$\frac{1}{2^{n - 1}}$
B.$\frac{1}{2^n}$
C.$\frac{1}{4^{n - 1}}$
D.$\frac{1}{4^n}$

答案： 10.C

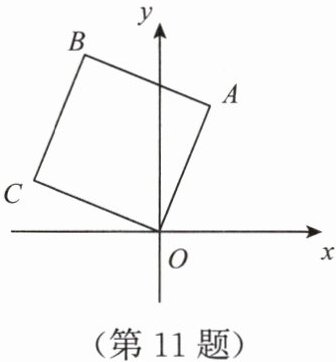
11. 如图，已知正方形 $OABC$ 顶点 $A$ 的坐标为 $(1, 3)$，则点 $C$ 的坐标为(-3,1)。

答案： 11.(-3,1)

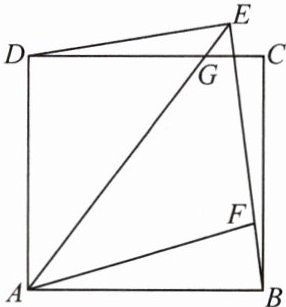
12. 如图，已知 $E$ 是正方形 $ABCD$ 的边 $CD$ 的中点，点 $F$ 在 $BC$ 上，且 $∠DAE = ∠FAE$，求证：$AF = AD + CF$。

答案：
12.证明：如图，过E作EG⊥AF，垂足为G.

∵∠DAE=∠FAE，
∠D=∠AGE=90°，
即AE为角平分线，ED⊥AD，EG⊥AG，
∴DE=EG.
在Rt△AEG和Rt△AED中，
$\begin{cases} EG = DE, \\ AE = AE, \end{cases}$
∴Rt△AEG≌Rt△AED(HL),
∴AG=AD.
∵E是CD的中点，
∴DE=EC=EG.
同理可知CF=GF.
∴AF=AG+GF=AD+CF.

如图①，在正方形 $ABCD$ 中，$AB = 4$，将三角尺放在正方形 $ABCD$ 上，使三角尺的直角顶点与点 $D$ 重合，三角尺的一边交 $AB$ 于点 $P$，另一边交 $BC$ 的延长线于点 $Q$。
(1) 求证：$AP = CQ$；
(2) 如图②，小明在图①的基础上作 $∠PDQ$ 的平分线 $DE$ 交 $BC$ 于点 $E$，连接 $PE$，他发现 $PE$ 和 $QE$ 存在一定的数量关系，请猜测他的结论，并予以证明；
(3) 在 (2) 的条件下，若 $AP = 1$，求 $PE$ 的长。

答案：
(1)证明：
∵四边形ABCD是正方形，
∴∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4.
∵∠PDQ=90°,
∴∠ADP=∠CDQ.
在△APD和△CQD中，$\begin{cases} ∠A = ∠DCQ, \\ AD = CD, \\ ∠ADP = ∠CDQ, \end{cases}$
∴△APD≌△CQD(ASA),
∴AP=CQ.
(2)解：PE=QE.理由如下：
由
(1)得△APD≌△CQD,
∴PD=QD.
∵DE平分∠PDQ,
∴∠PDE=∠QDE.
在△PDE和△QDE中，$\begin{cases} PD = QD, \\ ∠PDE = ∠QDE, \\ DE = DE, \end{cases}$
∴△PDE≌△QDE(SAS),
∴PE=QE.
(3)解：由
(2)得PE=QE，由
(1)得CQ=AP=1，
∴BQ=BC+CQ=5,BP=AB-AP=3.
设PE=QE=x，则BE=5-x，
在Rt△BPE中，由勾股定理得3^{2}+(5-x)^{2}=x^{2}，
解得x=3.4，
即PE的长为3.4.

(2024·呼和浩特)如图，正方形 $ABCD$ 的面积为 $50$，以 $AB$ 为腰作等腰三角形 $ABF$，$AB = AF$，$AE$ 平分 $∠DAF$ 交 $DC$ 于点 $G$，交 $BF$ 的延长线于点 $E$，连接 $DE$。若 $BF = 2$，则 $DG=$$\frac{15\sqrt{2}}{4}$。

答案： $\frac{15\sqrt{2}}{4}$