第76页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
9. 圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(如图),已知桌面的直径为 $1.2$ m,桌面距离地面 $1$ m,若灯泡距离地面 $3$ m,则地面上阴影部分的面积为
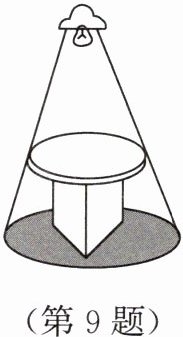
0.81\pi m^2
.
答案:
$9.0.81\pi m^2$
10. 如图,在 $\triangle ABC$ 中,$D$,$E$ 分别是 $AB$,$AC$ 上的点,$\triangle ADE\backsim\triangle ACB$,相似比为 $AD:AC = 2:3$,$\triangle ACB$ 的角平分线 $AF$ 交 $DE$ 于点 $G$,交 $BC$ 于点 $F$,求 $AG$ 与 $GF$ 的比.


答案:
10.解:
∵△ADE∽△ACB,
∴∠ADE=∠ACB,∠AED=∠ABC.
∵AF是∠BAC的平分线,
∴∠BAF=∠CAF.
∵∠AGD=∠CAF+∠AED,
∠AFC=∠BAF+∠ABC,
∴∠AGD=∠AFC
∴△AGD∽△AFC.
∵$\frac{AG}{AF}=\frac{AD}{AC}=\frac{2}{3} $
∴AG:GF=2:1.
∵△ADE∽△ACB,
∴∠ADE=∠ACB,∠AED=∠ABC.
∵AF是∠BAC的平分线,
∴∠BAF=∠CAF.
∵∠AGD=∠CAF+∠AED,
∠AFC=∠BAF+∠ABC,
∴∠AGD=∠AFC
∴△AGD∽△AFC.
∵$\frac{AG}{AF}=\frac{AD}{AC}=\frac{2}{3} $
∴AG:GF=2:1.
课堂·延伸
阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比 $(a:b)$.
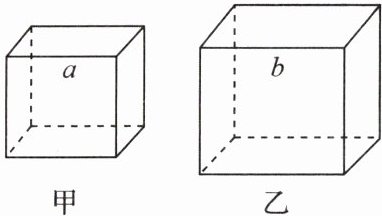
设 $S_{甲}$,$S_{乙}$ 分别表示这两个正方体的表面积,则 $\frac{S_{甲}}{S_{乙}}=\frac{6a^2}{6b^2}=(\frac{a}{b})^2$.
又设 $V_{甲}$,$V_{乙}$ 分别表示这两个正方体的体积,则 $\frac{V_{甲}}{V_{乙}}=\frac{a^3}{b^3}=(\frac{a}{b})^3$.
(1) 下列几何体中,一定属于相似体的是(
A. 两个球体
B. 两个锥体
C. 两个圆柱体
D. 两个长方体
(2) 请归纳出相似体的三条主要性质:
① 相似体的一切对应线段长的比等于
② 相似体表面积的比等于
③ 相似体体积的比等于
(3) 假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为 $1.1$ m,体重为 $18$ kg,到了九年级时,身高为 $1.65$ m,问他的体重是多少?(不考虑不同时期人体体平均密度的变化)
阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比 $(a:b)$.

设 $S_{甲}$,$S_{乙}$ 分别表示这两个正方体的表面积,则 $\frac{S_{甲}}{S_{乙}}=\frac{6a^2}{6b^2}=(\frac{a}{b})^2$.
又设 $V_{甲}$,$V_{乙}$ 分别表示这两个正方体的体积,则 $\frac{V_{甲}}{V_{乙}}=\frac{a^3}{b^3}=(\frac{a}{b})^3$.
(1) 下列几何体中,一定属于相似体的是(
A
).A. 两个球体
B. 两个锥体
C. 两个圆柱体
D. 两个长方体
(2) 请归纳出相似体的三条主要性质:
① 相似体的一切对应线段长的比等于
相似比
;② 相似体表面积的比等于
相似比的平方
;③ 相似体体积的比等于
相似比的立方
.(3) 假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为 $1.1$ m,体重为 $18$ kg,到了九年级时,身高为 $1.65$ m,问他的体重是多少?(不考虑不同时期人体体平均密度的变化)
答案:
解:
(1)A
(2)①相似比 ②相似比的平方 ③相似比的立方
(3)因为体重之比等于体积比,所以由题意知他的体积比为$(\frac{1.1}{1.65})^3.$
若设九年级时他的体重为x kg,
则有$(\frac{1.1}{1.65})^3=\frac{18}{x},$解得x=60.75.
答:九年级时他的体重为60.75kg.
(1)A
(2)①相似比 ②相似比的平方 ③相似比的立方
(3)因为体重之比等于体积比,所以由题意知他的体积比为$(\frac{1.1}{1.65})^3.$
若设九年级时他的体重为x kg,
则有$(\frac{1.1}{1.65})^3=\frac{18}{x},$解得x=60.75.
答:九年级时他的体重为60.75kg.
查看更多完整答案,请扫码查看


