《2025年初中同步练习册九年级数学上册北师大版北京师范大学出版社》

6. 如图，在 4×4 的正方形网格中，小正方形的边长均为 1，三角形的顶点都在格点上，则与△ABC 相似的三角形所在的网格图形是(B).

答案： 6.B

7. 把△ABC 的各边都扩大为原来的 4 倍，得到△A₁B₁C₁，则下列结论不正确的是(D).

A.△ABC ∽ △A₁B₁C₁
B.△ABC 和△A₁B₁C₁ 的各对应角相等
C.△ABC 与△A₁B₁C₁ 的相似比为$\frac{1}{4}$
D.△ABC 与△A₁B₁C₁ 的相似比为 4

答案： 7.D

8. 已知△ABC 的三边长分别为 3，$\sqrt{3}$，$\sqrt{15}$，△A₁B₁C₁ 的两边长分别为 1 和$\sqrt{5}$，当△A₁B₁C₁ 的第三边长为$\sqrt{3}$_ 时，△ABC 与△A₁B₁C₁ 相似.

答案： 8.$\sqrt{3}$

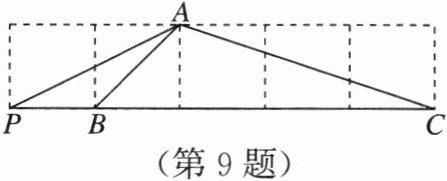
9. 如图，在边长为 1 的正方形网格中有点 P，A，B，C，则在图中所形成的三角形中，相似的三角形是△APB∽△CPA_.

答案： 9.△APB∽△CPA

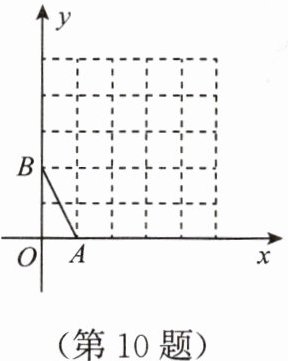
10. 在方格纸中，每个小方格的顶点称为格点，以格点连线为边的三角形叫做格点三角形，在如图所示的 5×5 方格纸中，作格点△ABC 与△OAB 相似（相似比不为 1），则 C 点坐标为(5,2)或(4,4)_.

答案： 10.(5,2)或(4,4)

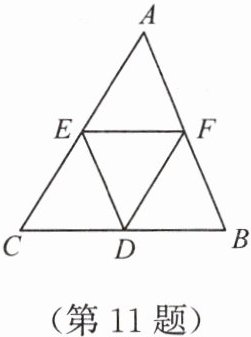
11. 如图，D，E，F 分别是△ABC 的三边 BC，CA，AB 的中点.
（1）求证：△DEF ∽ △ABC；
（2）写出图中其他几对相似的三角形.

答案： 11.
(1)证明:由题可知$DE=\frac{1}{2}AB$,$DF=\frac{1}{2}AC$,$EF=\frac{1}{2}BC$,
∴$\frac{DE}{AB}=\frac{DF}{AC}=\frac{EF}{BC}=\frac{1}{2}$.
∴△DEF∽△ABC;
(2)解:△AEF∽△ACB,△BDF∽△BCA,△DCE∽△BCA,△BDF∽△EFD,△BDF∽△FEA,△AEF∽△DFE,△DCE∽△FEA,△DCE∽△EFD,△DCE∽△BDF.

一个用钢筋做的三角架各边长分别是 30 cm，50 cm，70 cm，现在要做一个与其相似的钢筋三角架，而只有长 35 cm 和 70 cm 的两根钢筋，要求以其中一根为一边，从另一根上截下两段（允许有余料）作为另两边，问有几种不同的截法？

答案： 解:有两种不同的截法.
①设35cm长的线段为最长边,其他两边长分别为$x$cm和$y$cm,由$\frac{x}{30}=\frac{y}{50}=\frac{35}{70}$,得$x=15$,$y=25$,而15+25=40＜70,符合题意;
②设35cm长的线段为次长边,其他两边长分别为$a$cm和$b$cm,由$\frac{a}{30}=\frac{b}{70}=\frac{35}{50}$,得$a=21$,$b=49$,而21+49=70,符合题意;
③设35cm长的线段为最短边,经计算不符合题意.故有两种不同的截法