《2025年零障碍导教导学案九年级物理全一册沪粤版》

7. 将灯泡L和定值电阻R按图乙所示接入电路中,它们的电流随电压变化的图像如图甲。如果电路中电源电压是2 V,则下列结论正确的是(C)



A. 只闭合开关S,灯泡L的电功率为0.4 W
B. 闭合开关S、$S_1$后,电流表示数为0.6 A
C. 闭合开关S、$S_1$后,电阻R与灯泡L电功率之比为2:5
D. 闭合开关S、$S_1$后,20 s电路消耗的电能为20 J

答案： 解：A. 只闭合S时，电路为L的简单电路，电源电压2V，由图甲知L两端电压2V时电流0.5A，$P_L=U_LI_L=2V×0.5A=1W$，A错误。
B. 闭合S、S₁后，L与R并联，电源电压2V，L电压2V时电流0.5A；R为定值电阻，由图甲知其电压3V时电流0.3A，$R=\frac{U}{I}=\frac{3V}{0.3A}=10Ω$，电压2V时$I_R=\frac{2V}{10Ω}=0.2A$，干路电流$I=I_L+I_R=0.5A+0.2A=0.7A$，电流表示数0.7A，B错误。
C. $P_R=UI_R=2V×0.2A=0.4W$，$P_L=1W$，$P_R:P_L=0.4W:1W=2:5$，C正确。
D. $W=UIt=2V×0.7A×20s=28J$，D错误。
结论：正确的是C。
答案：C

8. 1840年,英国物理学家焦耳发现了通电导体产生的热量与电流、电阻和通电时间的关系。电熨斗是利用电流的热效应工作的。由于电热水器的功率远大于电冰箱的功率,从安全用电的角度考虑,电热水器的电源线比电冰箱的要粗(选填“粗”或“细”)。

答案： 【解析】：
这道题目主要考查了三个知识点：一是物理学史中关于通电导体产生热量的发现者；二是电流的热效应的应用；三是电阻与导线粗细的关系以及其在电器安全用电中的应用。
首先，需要知道1840年英国物理学家焦耳发现了通电导体产生的热量与电流、电阻和通电时间的关系，这是物理学史上的一个重要知识点。
其次，电熨斗是利用电流的热效应来工作的，这也是电流效应的一个重要应用。
最后，关于电热水器的电源线与电冰箱的电源线的粗细问题，需要理解电阻与导线粗细的关系。在电流和通电时间一定的情况下，电阻越大，产生的热量越多。而电阻与导线的材料、长度、横截面积和温度有关。在材料和长度一定的情况下，导线的横截面积越大，电阻越小。由于电热水器的功率远大于电冰箱的功率，根据$P = UI$，在电压一定的情况下，功率越大，电流越大。再根据$Q = I^{2}Rt$，电流越大，产生的热量越多，为了安全，需要减小电阻，因此电热水器的电源线应比电冰箱的电源线粗。
【答案】：
焦耳；热；粗。

9. 甲、乙两只节能灯的铭牌如图所示,将两灯串联在电路中,两灯都发光,乙(选填“甲”或“乙”)灯亮一些,如果将甲灯单独接入110 V电路中,它的实际功率为25W(忽略温度对节能灯电阻的影响)。此时甲灯的亮度比正常发光时要暗(选填“亮”或“暗”)。

答案： 【解析】：
本题可根据灯泡的铭牌信息，结合电功率公式分别求出两灯的电阻，再根据串联电路的特点和电功率公式判断两灯的亮度；根据电阻不变，结合电功率公式求出甲灯在$110V$电压下的实际功率，并与正常发光时的功率比较，判断其亮度变化。
判断两灯串联时哪盏灯更亮：
根据$P = \frac{U^{2}}{R}$（其中$P$为功率，$U$为电压，$R$为电阻）可得$R = \frac{U^{2}}{P}$。
甲灯的额定电压$U_{甲额}=220V$，额定功率$P_{甲额}=100W$，则甲灯的电阻$R_{甲}=\frac{U_{甲额}^{2}}{P_{甲额}}=\frac{(220V)^{2}}{100W}=484\Omega$。
乙灯的额定电压$U_{乙额}=220V$，额定功率$P_{乙额}=25W$，则乙灯的电阻$R_{乙}=\frac{U_{乙额}^{2}}{P_{乙额}}=\frac{(220V)^{2}}{25W}=1936\Omega$。
两灯串联时，通过它们的电流$I$相等，根据$P = I^{2}R$（其中$P$为功率，$I$为电流，$R$为电阻）可知，电阻大的灯泡实际功率大。
因为$R_{乙}＞R_{甲}$，所以乙灯的实际功率大，乙灯更亮。
求甲灯单独接入$110V$电路中的实际功率：
忽略温度对节能灯电阻的影响，甲灯的电阻$R_{甲}=484\Omega$不变，当甲灯接入$110V$电路中时，根据$P = \frac{U^{2}}{R}$可得甲灯的实际功率$P_{甲实}=\frac{U_{甲实}^{2}}{R_{甲}}=\frac{(110V)^{2}}{484\Omega}=25W$。
比较甲灯在$110V$电压下和正常发光时的亮度：
甲灯正常发光时的功率$P_{甲额}=100W$，而接入$110V$电路中时实际功率$P_{甲实}=25W$，因为$P_{甲实}＜P_{甲额}$，灯泡的亮度由实际功率决定，所以此时甲灯的亮度比正常发光时要暗。
【答案】：
乙；$25$；暗

10. 小明家有一个标有“220 V 880 W”的电炉,当它正常工作时的电阻是55Ω,通过电炉丝的电流为4A;在一次单独使用它时,小明家标有“1200 r/(kW·h)”的电能表在2 min的时间内铝盘转过了30转,则此时电炉的电功率是750W。

答案： 解：
1. 正常工作时的电阻：
由 $ P = \frac{U^2}{R} $ 得，$ R = \frac{U^2}{P} = \frac{(220\ V)^2}{880\ W} = 55\ \Omega $
2. 通过电炉丝的电流：
由 $ P = UI $ 得，$ I = \frac{P}{U} = \frac{880\ W}{220\ V} = 4\ A $
3. 此时电炉的电功率：
电能表转过30转消耗的电能 $ W = \frac{30}{1200}\ kW·h = 0.025\ kW·h $
时间 $ t = 2\ min = \frac{2}{60}\ h = \frac{1}{30}\ h $
电功率 $ P = \frac{W}{t} = \frac{0.025\ kW·h}{\frac{1}{30}\ h} = 0.75\ kW = 750\ W $
55；4；750

11. 甲、乙两个灯泡分别标有“220 V 40 W”“220 V 60 W”字样,并联在220 V电源上,通过灯丝电流较大的是乙灯泡,两灯电阻较大的是甲(前两空均选填“甲”或“乙”),使用相同时间,甲、乙两灯消耗的电能之比是2:3。

答案： 【解析】：
本题主要考查电功率公式、欧姆定律以及电能公式的应用。
首先，我们需要根据灯泡的额定电压和额定功率来计算它们的电阻和电流。
对于甲灯泡，标有“220 V 40 W”，其电阻$R_{甲}$可以通过公式$R = \frac{U^{2}}{P}$计算得出，电流$I_{甲}$可以通过公式$I = \frac{P}{U}$计算得出。
同理，对于乙灯泡，标有“220 V 60 W”，其电阻$R_{乙}$和电流$I_{乙}$也可以通过相同的公式计算得出。
由于两灯并联在220V电源上，所以它们两端的电压都等于220V，此时灯泡正常发光，实际功率等于额定功率，实际电流也等于额定电流，因此可以直接通过比较额定功率和额定电流来解答题目。
接下来，我们利用计算出的电阻和电流来解答题目中的各个问题。
1. 通过灯丝电流较大的灯泡：由于乙灯泡的额定功率大于甲灯泡的额定功率，且它们的额定电压相同，所以根据公式$I = \frac{P}{U}$，我们可以得出通过乙灯泡灯丝的电流较大。
2. 电阻较大的灯泡：同样地，由于甲灯泡的额定功率小于乙灯泡的额定功率，且它们的额定电压相同，所以根据公式$R = \frac{U^{2}}{P}$，我们可以得出甲灯泡的电阻较大。
3. 使用相同时间，甲、乙两灯消耗的电能之比：电能可以通过公式$W = Pt$计算得出。由于甲、乙两灯的额定功率之比为$\frac{40W}{60W} = \frac{2}{3}$，且使用时间相同，所以甲、乙两灯消耗的电能之比也为$\frac{2}{3}$。
【答案】：
乙；甲；$2:3$。

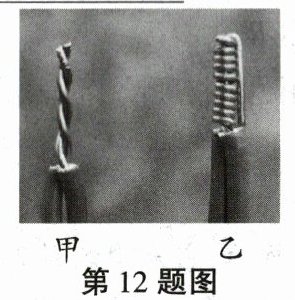
12. 如图所示为导线的两种接法,连接段电阻较大的是甲图,在相同电路中,更容易出现故障的是甲图,若图乙连接段导线电阻为$2.5×10^{-4}\ \Omega$,电路电流为0.2 A,则1 min内此连接段产生的热量为$6×10^{-3}$J。

答案： 解：甲；甲；6×10^{-3}
步骤：
1. 甲图连接段电阻较大，因接触面积小、接触点少，电阻大。
2. 甲图更容易出现故障，电阻大导致发热多，易损坏。
3. 热量计算：Q=I²Rt=(0.2 A)²×2.5×10^{-4} Ω×60 s=6×10^{-3} J。

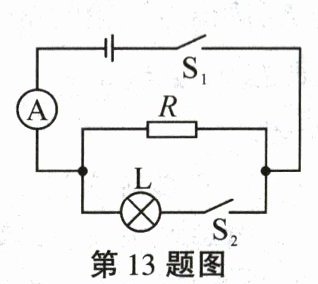
13. 如图所示,电源电压恒定不变,电阻R的阻值为10 Ω。闭合开关$S_1和S_2$时,电阻R和灯L是并联的;在对$S_2$进行闭合或断开的操作中,电流表可测得0.9 A和0.6 A两个值,则电源电压为6V,灯L发光时的功率为1.8W。

答案： 解：并；6；1.8
步骤：
1. 闭合开关S₁和S₂时，电流从电源正极出发，分两支分别流经电阻R和灯L，再汇合回到电源负极，故R和L是并联。
2. 只闭合S₁时，电路为R的简单电路，电流I₁=U/R=U/10Ω；闭合S₁和S₂时，R与L并联，总电流I₂=U/R + U/R_L，因并联总电阻小于R，所以I₂＞I₁。已知电流值为0.9A和0.6A，故I₁=0.6A，I₂=0.9A。
3. 由I₁=U/R得，电源电压U=I₁R=0.6A×10Ω=6V。
4. 通过L的电流I_L=I₂ - I₁=0.9A - 0.6A=0.3A，灯L发光时的功率P=UI_L=6V×0.3A=1.8W。

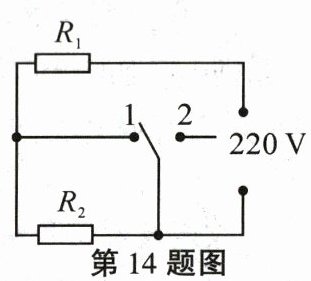
14. 某款电饭煲有加热和保温两挡。其电路如图所示,已知$R_1= 88\ \Omega$,$R_2= 2112\ \Omega$。开关S置于2(选填“1”或“2”)时是保温挡,保温10 min产生的热量是13200J;高温挡的功率是550W。

答案： 【解析】：
本题可根据电路连接情况结合$P = \frac{U^{2}}{R}$判断电饭煲的挡位，再根据焦耳定律计算保温挡产生的热量，根据$P = \frac{U^{2}}{R}$计算高温挡的功率。
1. 判断保温挡时开关的位置：
根据$P = \frac{U^{2}}{R}$（其中$P$为功率，$U$为电压，$R$为电阻）可知，在电源电压$U$一定时，电阻$R$越大，功率$P$越小。
当开关$S$置于$2$时，$R_1$与$R_2$串联，此时电路中的总电阻$R_{串}=R_1 + R_2$；当开关$S$置于$1$时，只有$R_1$接入电路，此时电路中的电阻$R = R_1$。
因为$R_{串}＞R_1$，所以开关$S$置于$2$时，电路电阻大，功率小，电饭煲处于保温挡。
2. 计算保温$10\ min$产生的热量：
当开关$S$置于$2$时，$R_1$与$R_2$串联，总电阻$R_{总}=R_1 + R_2 = 88\ \Omega + 2112\ \Omega = 2200\ \Omega$。
家庭电路电压$U = 220\ V$，时间$t = 10\ min = 10×60\ s = 600\ s$。
根据焦耳定律$Q = \frac{U^{2}}{R}t$，可得保温$10\ min$产生的热量$Q = \frac{(220\ V)^{2}}{2200\ \Omega}×600\ s = 13200\ J$。
3. 计算高温挡的功率：
当开关$S$置于$1$时，只有$R_1$接入电路，此时为高温挡。
根据$P = \frac{U^{2}}{R}$，可得高温挡的功率$P_{高}=\frac{(220\ V)^{2}}{88\ \Omega}= 550\ W$。
【答案】：
2；13200；550