《2025年零障碍导教导学案九年级物理全一册沪粤版》

7. 如图甲所示是体育课上坐位体前屈测量仪,图乙是小雅设计的模拟电路,闭合开关,当推动绝缘柄使滑动变阻器的滑块向左移动,可利用示数增大的电表反映测量成绩。在此测试过程中下列分析正确的是(B)

A.绝缘柄向左推的距离越大,滑动变阻器的电阻越大
B.绝缘柄向左推的距离越大,电压表示数越大
C.绝缘柄向左推时电流表示数变小,电压表变大
D.此电路设计中,用电流表示数反映测量成绩

答案： 【解析】：
本题主要考查了滑动变阻器的使用、欧姆定律的应用以及串联电路的特点，根据滑动变阻器的移动分析电路中电阻的变化，再根据欧姆定律和串联电路的特点分析电路中电流和电压的变化。
由电路图可知，$R_1$与$R_2$串联，电压表测$R_1$两端的电压，电流表测电路中的电流。
A选项：绝缘柄向左推的距离越大，滑动变阻器$R_1$接入电路中的电阻越小，故A错误。
B选项：绝缘柄向左推的距离越大，$R_1$电阻变小，电路中的总电阻变小，由$I=\frac{U}{R}$可知，电路中的电流变大，由$U=IR$可知，$R_2$两端的电压变大，因串联电路中总电压等于各分电压之和，所以，$R_1$两端的电压变大，即电压表的示数变大，故B正确。
C选项：绝缘柄向左推时，$R_1$电阻变小，电路中的总电阻变小，由$I=\frac{U}{R}$可知，电路中的电流变大，即电流表的示数变大，由B选项分析可知，电压表的示数也变大，故C错误。
D选项：由B选项分析可知，绝缘柄向左移动时，电压表示数增大，可利用示数增大的电表反映测量成绩，即用电压表示数反映测量成绩，故D错误。
【答案】：B。

8. 某段导体两端的电压为3 V时,通过它的电流为0.6 A,则该导体的电阻为5Ω；当导体两端的电压减小一半时,则该导体的电阻为5Ω；当电路断开时,导体的电阻为5Ω。

答案： 【解析】：
本题考查欧姆定律的应用以及电阻的性质。
首先，我们利用欧姆定律来计算导体的电阻。欧姆定律的公式为$R = \frac{U}{I}$，其中$R$是电阻，$U$是电压，$I$是电流。
根据题目给出的数据，当导体两端的电压为3V，通过它的电流为0.6A时，我们可以将这些值代入欧姆定律的公式中计算电阻。
其次，我们需要理解电阻的性质。电阻是导体本身的属性，与加在导体两端的电压和通过导体的电流无关。
因此，无论电压如何变化，或者电路是否断开，导体的电阻都不会改变。
【答案】：
根据欧姆定律，该导体的电阻为$R = \frac{U}{I} = \frac{3V}{0.6A} = 5\Omega$。
由于电阻是导体本身的属性，与电压和电流无关，所以当导体两端的电压减小一半时，或者电路断开时，导体的电阻仍然是$5\Omega$。
故答案为：$5\Omega$；$5\Omega$；$5\Omega$。

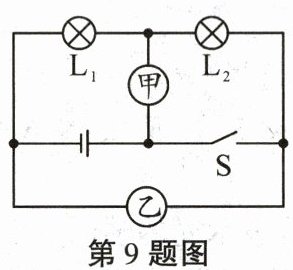
9. 如图所示,若开关S闭合后,灯$ L_1 $、$ L_2 $都能发光,则甲是 电压表(选填“电压表”或“电流表”),此时$ L_1 $、$ L_2 $的连接方式是 并(选填“串”或“并”)联；若开关S断开后,两灯都能发光,甲、乙两表的示数之比为4∶3,则灯$ L_1 $、$ L_2 $电阻之比为 1:3。

答案： 1. 首先判断开关$S$闭合时：
若开关$S$闭合后，灯$L_1$、$L_2$都能发光，因为电流表相当于导线，电压表相当于开路，若甲是电流表，会使$L_2$短路，所以甲是电压表；此时电流有两条路径，分别经过$L_1$和$L_2$，所以$L_1$、$L_2$的连接方式是并联。
2. 然后判断开关$S$断开时：
若开关$S$断开后，两灯都能发光，此时$L_1$、$L_2$串联，甲表测电源电压$U$，乙表测$L_2$两端电压$U_2$。
已知$\frac{U}{U_2}=\frac{4}{3}$，根据串联电路电压特点$U = U_1+U_2$，则$\frac{U_1}{U_2}=\frac{U - U_2}{U_2}=\frac{4 - 3}{3}=\frac{1}{3}$。
再根据串联电路电流特点$I = I_1 = I_2$，由$I=\frac{U}{R}$可得$R=\frac{U}{I}$，那么$\frac{R_1}{R_2}=\frac{\frac{U_1}{I}}{\frac{U_2}{I}}=\frac{U_1}{U_2}$（因为$I$相同）。
所以答案依次为：电压表；并；$1:3$。

10. 如图甲所示电路,开关$ S_1 $、$ S_2 $闭合后两电流表的指针均指在同一位置,示数如图乙所示,则通过$ R_1 $的电流为 1.44 A,两电阻之比$ R_1:R_2 $ = 1:4；只断开开关$ S_2 $,电流表$ A_1 $的示数将 变小(选填“变大”“变小”或“不变”)。

答案： 1. 首先分析电流表量程和读数：
由电路图可知，$R_1$与$R_2$并联，电流表$A_1$测干路电流，电流表$A_2$测$R_2$支路的电流。
因为并联电路中干路电流等于各支路电流之和，且两电流表的指针均指在同一位置，所以电流表$A_1$的量程为$0 - 3A$，分度值为$0.1A$，示数$I = 1.8A$；电流表$A_2$的量程为$0 - 0.6A$，分度值为$0.02A$，示数$I_2=0.36A$。
2. 然后求通过$R_1$的电流：
根据并联电路电流规律$I = I_1+I_2$，可得通过$R_1$的电流$I_1=I - I_2$。
把$I = 1.8A$，$I_2 = 0.36A$代入得$I_1=1.8A - 0.36A=1.44A$。
3. 接着求两电阻之比：
根据并联电路的电压特点$U = U_1 = U_2$，由$I=\frac{U}{R}$可得$U = I_1R_1=I_2R_2$。
则$\frac{R_1}{R_2}=\frac{I_2}{I_1}$，把$I_1 = 1.44A$，$I_2 = 0.36A$代入得$\frac{R_1}{R_2}=\frac{0.36A}{1.44A}=\frac{1}{4}$。
4. 最后分析只断开开关$S_2$时电流表$A_1$示数的变化：
只断开开关$S_2$时，电路变为$R_2$的简单电路，电流表$A_1$测通过$R_2$的电流。
因为并联电路中各支路独立工作、互不影响，所以通过$R_2$的电流不变（$R_2$两端电压不变，$R_2$电阻不变，根据$I=\frac{U}{R}$，$I_2$不变），即电流表$A_1$的示数变小（原来测干路电流，现在测$R_2$支路电流）。
故答案依次为：$1.44$；$1:4$；变小。

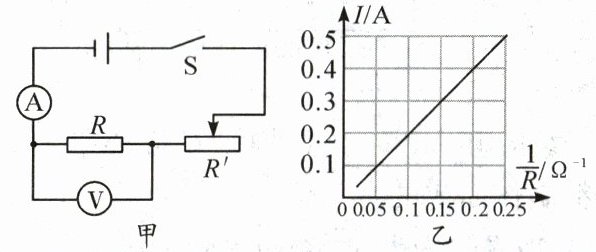
11. 小明利用如图甲所示的电路探究通过导体的电流与电阻的关系,这个实验中要控制 导体两端的电压 一定,根据实验的数据绘出了$ I-\frac{1}{R} $图像,如图乙所示。分析图像可知,当导体的电阻为 20 Ω时,通过它的电流为0.1 A；实验过程中,小明控制导体两端的电压为 2 V。

答案： 【解析】：
本题主要考查了欧姆定律的应用以及对控制变量法的理解，通过分析$I-\frac{1}{R}$图像来求解电阻和电压。
在探究通过导体的电流与电阻的关系时，要采用控制变量法，控制导体两端的电压一定。
从$I-\frac{1}{R}$图像中可以看出，电流$I$与$\frac{1}{R}$成正比关系。
根据$I=\frac{U}{R}$变形可得$I = U×\frac{1}{R}$，图像的斜率就表示导体两端的电压$U$。
当$I = 0.2A$时，$\frac{1}{R}=0.1\Omega^{-1}$，则$U = \frac{I}{\frac{1}{R}}=\frac{0.2A}{0.1\Omega^{-1}} = 2V$。
当$I = 0.1A$时，因为$U = 2V$，根据$R=\frac{U}{I}$，可得$R=\frac{2V}{0.1A}=20\Omega$。
【答案】：
导体两端的电压；20；2

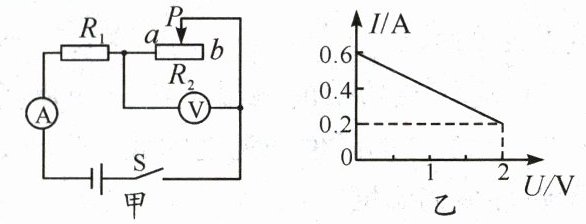
12. 如图甲所示的电路中,$ R_1 $为定值电阻,$ R_2 $为滑动变阻器,电源电压不变。闭合开关S后,滑片P从a端移动到b端,电流表示数I与电压表示数U的变化关系如图乙所示,则电源电压为 3 V,$ R_1 $的阻值为 5 Ω,$ R_2 $的最大阻值为 10 Ω。

答案： 【解析】：
本题可根据串联电路的特点和欧姆定律，结合图像信息来求解电源电压、定值电阻$R_1$的阻值以及滑动变阻器$R_2$的最大阻值。
步骤一：分析电路连接方式及电表测量对象
由图甲可知，定值电阻$R_1$与滑动变阻器$R_2$串联，电流表测量电路中的电流，电压表测量滑动变阻器$R_2$两端的电压。
步骤二：求电源电压和$R_1$的阻值
当滑片$P$位于$a$端时，滑动变阻器接入电路的电阻为$0$，此时电路中只有$R_1$，电路中的电流最大。
由图乙可知，此时电路中的电流$I_{max}=0.6A$，根据欧姆定律$I = \frac{U}{R}$可得，电源电压$U = I_{max}R_1 = 0.6A× R_1$ ①。
当滑片$P$位于$b$端时，滑动变阻器接入电路的电阻最大，此时电路中的电流最小，电压表的示数最大。
由图乙可知，此时电路中的电流$I_{min}=0.2A$，电压表的示数$U_2 = 2V$。
根据串联电路的电压特点$U = U_1 + U_2$以及欧姆定律$U_1 = I_{min}R_1$，可得电源电压$U = I_{min}R_1 + U_2 = 0.2A× R_1 + 2V$ ②。
联立①②可得方程组$\begin{cases}U = 0.6A× R_1\\U = 0.2A× R_1 + 2V\end{cases}$，解方程组：
将$U = 0.6A× R_1$代入$U = 0.2A× R_1 + 2V$中，得到$0.6A× R_1 = 0.2A× R_1 + 2V$，
移项可得$0.6A× R_1 - 0.2A× R_1 = 2V$，
即$0.4A× R_1 = 2V$，
解得$R_1 = \frac{2V}{0.4A} = 5\Omega$。
将$R_1 = 5\Omega$代入$U = 0.6A× R_1$，可得$U = 0.6A× 5\Omega = 3V$。
步骤三：求$R_2$的最大阻值
当滑片$P$位于$b$端时，滑动变阻器接入电路的电阻最大，此时电路中的电流$I_{min}=0.2A$，电压表的示数$U_2 = 2V$。
根据欧姆定律$R = \frac{U}{I}$，可得$R_2$的最大阻值$R_{2max} = \frac{U_2}{I_{min}} = \frac{2V}{0.2A} = 10\Omega$。
【答案】：
电源电压为$3V$，$R_1$的阻值为$5\Omega$，$R_2$的最大阻值为$10\Omega$。