第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 想一想,填一填。


=
蝴蝶
蜻蜓
蜻蜓
蝴蝶
=
20
100
5
100
答案:
= 蝴蝶 蜻蜓 蜻蜓 蝴蝶
= 20 100 5 100
= 20 100 5 100
25+18= 18+
298+73= 73+
48×271=
120×31=
25
298+73= 73+
298
48×271=
271
×48120×31=
31
×120
答案:
25 298 271 31
(1)25×11×4= 25×4×11,这里运用的运算律是(
A.加法交换律
B.乘法交换律
C.无法确定
B
)。A.加法交换律
B.乘法交换律
C.无法确定
答案:
B
(2)加法交换律会改变( )。
A.计算结果
B.数的位置
C.数的大小
A.计算结果
B.数的位置
C.数的大小
答案:
B
(3)加法交换律的应用很广泛,下面的选项中,没有运用到加法交换律的是( )。
A.
B. △+□= □+△
C.
A.

B. △+□= □+△
C.

答案:
A
4. 用竖式计算下面各题,并用加法交换律或乘法交换律进行验算。
927+218 验算:
78×25 验算:
927+218 验算:
78×25 验算:
答案:
927+218=1145
9 2 7
+ 2 1 8
1 1 4 5
验算: 2 1 8
+ 9 2 7
1 1 4 5

78×25=1950
7 8
× 2 5
3 9 0
1 5 6
1 9 5 0
验算: 2 5
× 7 8
2 0 0
1 7 5
1 9 5 0

927+218=1145
9 2 7
+ 2 1 8
1 1 4 5
验算: 2 1 8
+ 9 2 7
1 1 4 5

78×25=1950
7 8
× 2 5
3 9 0
1 5 6
1 9 5 0
验算: 2 5
× 7 8
2 0 0
1 7 5
1 9 5 0

5.(算法探究)想一想,填一填。
437+652= 457+6
336+663= 333+
423+156= 123+
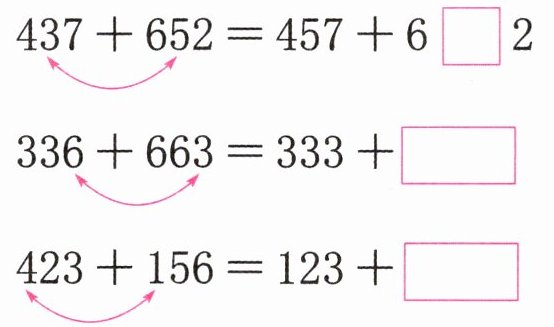
我发现:交换两个加数相同数位上的数字,它们的和(
445+2
3
437+652= 457+6
3
2336+663= 333+
666
423+156= 123+
456
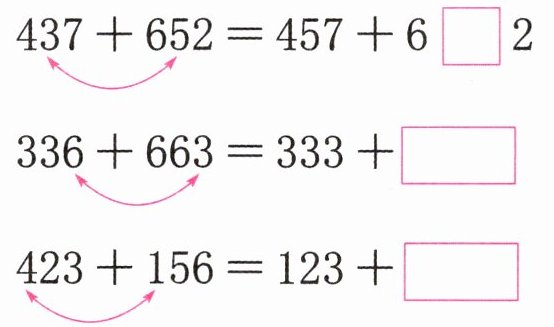
我发现:交换两个加数相同数位上的数字,它们的和(
相等
)。请你用这个发现填写下面两个算式。445+2
3
2= 432+245
3
7
4+58
= 35
8+74
答案:
3 666 456 相等 3 5 7 8 5 4
解析:交换两个加数相同数位上的数字,它们的和相等,通过对比等号两边的加数得到结果。
解析:交换两个加数相同数位上的数字,它们的和相等,通过对比等号两边的加数得到结果。
查看更多完整答案,请扫码查看


