1.____的两个三角形全等(可以简写成“边角边”或“____”).
答案:
两边及其夹角分别相等 SAS
2.新情境测量壶底内径(2025·浙江台州路桥区期末)
如图(1)是路桥博物馆中的纹青釉点彩盘口壶,其示意图如图(2)所示,为了测量其底部内径CD,考古学家将两根细木条的中点固定在一起,量出A,B两点之间的距离,即可得到CD的长度,其依据的数学基本事实是( ).
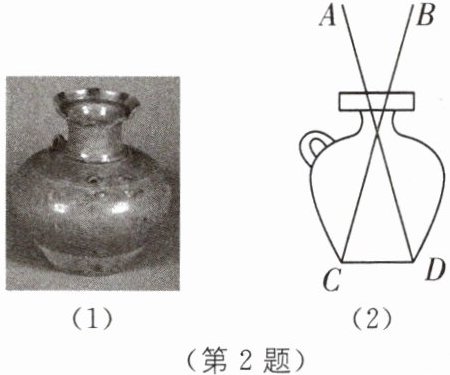
A.三边分别相等的两个三角形全等
B.两边和它们的夹角分别相等的两个三角形全等
C.两角和它们的夹边分别相等的两个三角形全等
D.两点之间,线段最短
如图(1)是路桥博物馆中的纹青釉点彩盘口壶,其示意图如图(2)所示,为了测量其底部内径CD,考古学家将两根细木条的中点固定在一起,量出A,B两点之间的距离,即可得到CD的长度,其依据的数学基本事实是( ).

A.三边分别相等的两个三角形全等
B.两边和它们的夹角分别相等的两个三角形全等
C.两角和它们的夹边分别相等的两个三角形全等
D.两点之间,线段最短
答案:
B
3.中考新考法满足结论的条件开放(2024·镇江丹阳期中)如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”,则需要添加的条件是____.
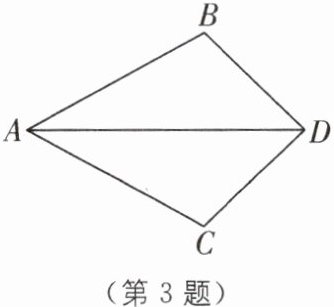

答案:
AB=AC
4.(2025·山东菏泽期末)如图,在△ABC中,AB= AC,点D为BC边上一点,点E在边AC上,BD= CE,AC= DC,∠BAC= 80°,则∠ADE的度数为____.
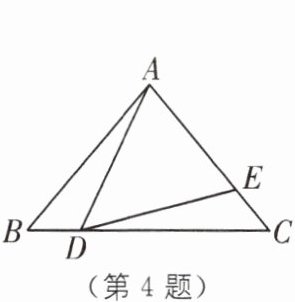

答案:
50°
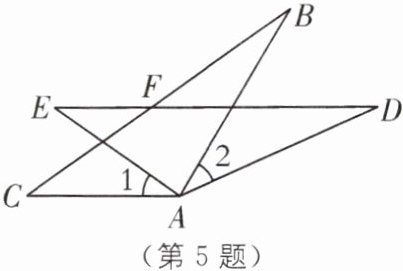
5.(2025·无锡惠山区期末)如图,AC= AE,∠1= ∠2,AB= AD.
(1)求证:△ABC≌△ADE;
(2)若BC= 15,EF= 5,则DF= ____.
(1)求证:△ABC≌△ADE;
(2)若BC= 15,EF= 5,则DF= ____.

答案:
(1)
∵∠1=∠2,
∴∠CAB=∠EAD.在△CAB和△EAD中,{AC=AE,∠CAB=∠EAD,AB=AD,
∴△CAB≌△EAD(SAS).
(2)10
(1)
∵∠1=∠2,
∴∠CAB=∠EAD.在△CAB和△EAD中,{AC=AE,∠CAB=∠EAD,AB=AD,
∴△CAB≌△EAD(SAS).
(2)10
6.提分优练如图,在△AOB和△COD中,OA= OB,OC= OD,OA<OC,∠AOB= ∠COD= 36°.连接AC,BD交于点M,连接OM.
(1)求证:AC= BD;
(2)求∠AMB的度数.

(1)求证:AC= BD;
(2)求∠AMB的度数.

答案:
(1)
∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD.在△AOC和△BOD中,{OA=OB,∠AOC=∠BOD,OC=OD,
∴△AOC≌△BOD(SAS),
∴AC=BD.
(2)由
(1),得∠OAC=∠OBD,由三角形外角的性质,得∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°.
(1)
∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD.在△AOC和△BOD中,{OA=OB,∠AOC=∠BOD,OC=OD,
∴△AOC≌△BOD(SAS),
∴AC=BD.
(2)由
(1),得∠OAC=∠OBD,由三角形外角的性质,得∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°.
查看更多完整答案,请扫码查看


