1. 在 $ Rt\triangle ABC $ 中, $ \angle C = 90^{\circ} $, 设 $ \angle A $ 的对边是 $ a $, $ \angle B $ 的对边是 $ b $, $ \angle C $ 的对边是 $ c $, 则____$ ^{2} + $____$ ^{2} = $____$ ^{2} $.
答案:
a b c
2. 解决直角三角形中线段求值的问题,通常要用到勾股定理,如果没有直角三角形,那么可以通过添加辅助线来构造____,再利用勾股定理解决上述问题.
答案:
直角三角形
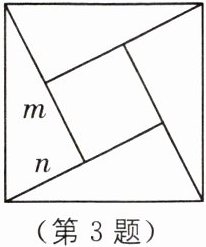
3. (2025·无锡滨湖区期末)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为 $ m,n(m > n) $. 若小正方形面积为 7, $ (m + n)^{2} = 21 $, 则大正方形面积为( ).
A.11
B.12
C.13
D.14

A.11
B.12
C.13
D.14
答案:
D
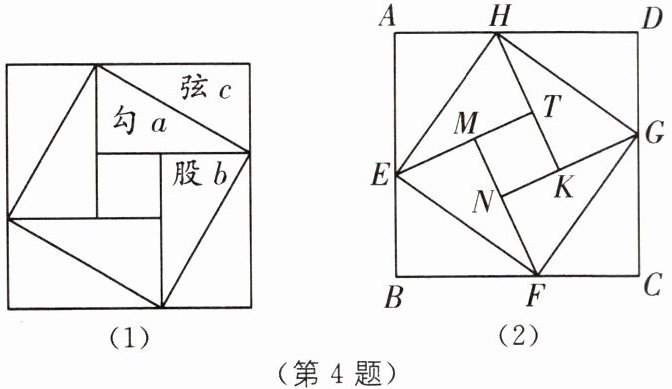
4. 传统文化 赵爽弦图 (2025·浙江金华永康期中)我国古代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(图(1)),后人称其为“赵爽弦图”.由图(1)变化得到图(2),它是用八个全等的直角三角形拼接而成的,记图中正方形 $ ABCD $, 正方形 $ EFGH $, 正方形 $ MNKT $ 的面积分别为 $ S_{1},S_{2},S_{3} $. 若 $ S_{2} = 6 $, 则 $ S_{1} + S_{3} $ 的值为____.

答案:
12
5. 提分优练 (2024·无锡江阴期中)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽发现的“弦图”,它是由四个大小相等,形状相同的直角三角形与中间的小正方形拼成的一个大正方形(如图(1)),设直角三角形的较短直角边为 $ a $, 较长直角边为 $ b $, 最长的斜边为 $ c $.
(1) 若 $ a = 6,b = 8 $, 则图(1)中大正方形的面积为____;
(2) 猜想 $ a^{2},b^{2},c^{2} $ 之间的数量关系,并按给出的格式说明理由.
$ \because S_{大正方形} = $____, $ S_{大正方形} = 4 × \frac{1}{2}ab + $____$ = $____, $ \therefore $____;
(3) 若图(1)中大正方形的面积是 15,小正方形的面积是 1,现将四个直角三角形按如图(2)的形式重新摆放,求图(2)中最大的正方形的面积.

(1) 若 $ a = 6,b = 8 $, 则图(1)中大正方形的面积为____;
(2) 猜想 $ a^{2},b^{2},c^{2} $ 之间的数量关系,并按给出的格式说明理由.
$ \because S_{大正方形} = $____, $ S_{大正方形} = 4 × \frac{1}{2}ab + $____$ = $____, $ \therefore $____;
(3) 若图(1)中大正方形的面积是 15,小正方形的面积是 1,现将四个直角三角形按如图(2)的形式重新摆放,求图(2)中最大的正方形的面积.

答案:
(1)100
(2)$c^{2}$ $(a-b)^{2}$ $a^{2}+b^{2}$ $a^{2}+b^{2}=c^{2}$
(3)
∵题图
(1)中大正方形的面积是15,
$\therefore a^{2}+b^{2}=c^{2}=15.$
∵小正方形的面积是1,
$\therefore (a-b)^{2}=a^{2}+b^{2}-2ab=1,\therefore ab=7,$
∴题图
(2)中最大的正方形的面积为$c^{2}+4×\frac {1}{2}ab=15+$
$2×7=29.$
(1)100
(2)$c^{2}$ $(a-b)^{2}$ $a^{2}+b^{2}$ $a^{2}+b^{2}=c^{2}$
(3)
∵题图
(1)中大正方形的面积是15,
$\therefore a^{2}+b^{2}=c^{2}=15.$
∵小正方形的面积是1,
$\therefore (a-b)^{2}=a^{2}+b^{2}-2ab=1,\therefore ab=7,$
∴题图
(2)中最大的正方形的面积为$c^{2}+4×\frac {1}{2}ab=15+$
$2×7=29.$
查看更多完整答案,请扫码查看


