《2025年课时训练江苏人民出版社八年级数学上册苏科版》

1. 无限____小数称为无理数.

答案： 不循环

2. 有理数和无理数统称为____.

答案： 实数

3. 每一个实数都可以用数轴上的一个____来表示；反过来,数轴上的每一个____都表示一个实数. 实数与____一一对应.

答案： 点 点 数轴上的点

4. (2025·广东江门期中)在下列实数：$0,\sqrt {2.5},-3.1415,\sqrt {4},\frac {22}{3},0.343343334…$(每两个4之间依次多一个3)中,无理数有( ).

A.1个
B.2个
C.3个
D.4个

答案： B

5. 中考新考法 规律探究 (2025·浙江宁波期中)正方形 ABCD 在数轴上的位置如图所示,点 D,A 对应的数分别为 0 和 1. 若正方形 ABCD 绕着顶点顺时针方向在数轴上连续翻转,翻转 1 次后,点 B 所对应的数为 2,则翻转 2024 次后,数轴上数 2025 所对应的点是( ).


A.点 A
B.点 B
C.点 C
D.点 D

答案： A

6. (2025·济南历下区二模)实数 a,b,c 在数轴上对应点的位置如图所示,下列式子正确的是( ).


A.$a+c＞a+b$
B.$(b-a)(b-c)＞0$
C.$ac＞ab$
D.$c-b＞c-a$

答案： D

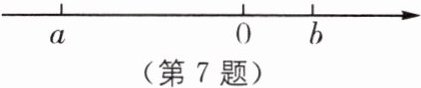
7. (2025·湖南长沙望城区期中改编)如图,在数轴上的两个点表示为实数 a,b,化简：$\sqrt {(a-b)^{2}}-|a+b|+\sqrt [3]{a^{3}}.$

答案： 由数轴，可得a＜0＜b，|a|＞|b|，
则a−b＜0，a+b＜0，
原式=b−a−[−(a+b)]+a
=b−a+a+b+a
=a+2b.

8. 提分优练 (2025·广东深圳宝安区期末)阅读下面的文字,解答问题：
我们知道$\sqrt {3}$是无理数,无理数是无限不循环小数,因此不能将$\sqrt {3}$的小数部分全部写出来,于是小慧用$\sqrt {3}-1来表示\sqrt {3}$的小数部分,你明白小慧的表示方法吗？
事实上,因为$\sqrt {3}$的整数部分是 1,将一个数减去它的整数部分,差就是小数部分.
例如：$\because \sqrt {4}＜\sqrt {7}＜\sqrt {9}$,即$2＜\sqrt {7}＜3,$
$\therefore \sqrt {7}$的整数部分为 2,小数部分为$\sqrt {7}-2.$
请解答：(1)$\sqrt {5}$的整数部分是____,小数部分是____.
(2)已知 x 是$8+\sqrt {11}$的整数部分,y 是$8+\sqrt {11}$的小数部分,求$x-y$的值.

答案： （1）2 √5−2
（2）
∵√9＜√11＜√16，即3＜√11＜4，
∴11＜8+√11＜12，
∴8+√11的整数部分为11，小数部分为8+√11−11=√11−3，即x=11，y=√11−3，
∴x−y=11−(√11−3)=11−√11+3=14−√11.