1. 两个能______的三角形叫作全等三角形. “全等”用符号“______”表示.
答案:
完全重合 ≌
2. 表示两个三角形全等时,通常把对应顶点的字母写在______的位置上.
答案:
对应
3. 全等三角形的性质:全等三角形的______边相等,______角相等.
答案:
对应 对应
4. (2024·广东惠州期末)下列汽车标志中,不是由多个全等图形组成的是( ).


答案:
B
5. (2025·南通如皋期末)如图,$△ABC≌△DEF$,$∠A= 36^{\circ}$,$∠E= 84^{\circ}$,则$∠F$的度数为( ).

A.$36^{\circ}$
B.$60^{\circ}$
C.$84^{\circ}$
D.$120^{\circ}$

A.$36^{\circ}$
B.$60^{\circ}$
C.$84^{\circ}$
D.$120^{\circ}$
答案:
B
6. (2024·陕西安康期末)如图,已知$△OAB≌△OCD$,$∠A= 30^{\circ}$,$∠AOB= 105^{\circ}$,则$∠D= $______$^{\circ}$.
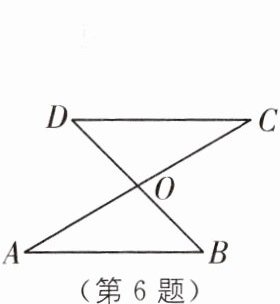

答案:
45
7. (2024·成都中考)如图,$△ABC≌△CDE$,若$∠D= 35^{\circ}$,$∠ACB= 45^{\circ}$,则$∠DCE$的度数为______.
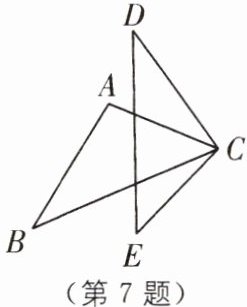

答案:
100°
8. (2025·浙江绍兴诸暨期末)如图,已知$△ABC≌△DEF$,点$B$,$E$,$C$,$F$在同一直线上.
(1)若$∠A= 95^{\circ}$,$∠F= 55^{\circ}$,求$∠DEF$的度数;
(2)若$BC= 6$,点$E是BC$的中点,求$CF$的长.

(1)若$∠A= 95^{\circ}$,$∠F= 55^{\circ}$,求$∠DEF$的度数;
(2)若$BC= 6$,点$E是BC$的中点,求$CF$的长.

答案:
(1)
∵△ABC≌△DEF,
∴∠A=∠D=95°,
∴∠DEF=180°-∠D-∠F=180°-95°-55°=30°.
(2)
∵△ABC≌△DEF,
∴BC=EF=6.
∵点 E 是 BC 的中点,
∴CE=$\frac{1}{2}$BC=3,
∴CF=EF-CE=6-3=3.
(1)
∵△ABC≌△DEF,
∴∠A=∠D=95°,
∴∠DEF=180°-∠D-∠F=180°-95°-55°=30°.
(2)
∵△ABC≌△DEF,
∴BC=EF=6.
∵点 E 是 BC 的中点,
∴CE=$\frac{1}{2}$BC=3,
∴CF=EF-CE=6-3=3.
9. 提分优练 如图,点$A$,$B$,$C$在同一直线上,点$E在BD$上,且$△ABD≌△EBC$.
(1)若$AB= 2$,$BC= 3$,求$DE$的长;
(2)判断$AD与CE$所在直线的位置关系,并说明理由.

(1)若$AB= 2$,$BC= 3$,求$DE$的长;
(2)判断$AD与CE$所在直线的位置关系,并说明理由.

答案:
(1)
∵△ABD≌△EBC,AB=2,BC=3,
∴EB=AB=2,BD=BC=3.
∵点 E 在 BD 上,
∴DE=BD-BE=3-2=1.
(2)AD⊥CE.理由如下:
∵点 A,B,C 在同一直线上,且△ABD≌△EBC,
∴∠ABD=∠EBC=90°,∠D=∠C.延长 CE 交 AD 于点 F.
∵∠DEF=∠CEB,
∴∠DFE=∠CBE=90°,
∴AD⊥CE.
(1)
∵△ABD≌△EBC,AB=2,BC=3,
∴EB=AB=2,BD=BC=3.
∵点 E 在 BD 上,
∴DE=BD-BE=3-2=1.
(2)AD⊥CE.理由如下:
∵点 A,B,C 在同一直线上,且△ABD≌△EBC,
∴∠ABD=∠EBC=90°,∠D=∠C.延长 CE 交 AD 于点 F.
∵∠DEF=∠CEB,
∴∠DFE=∠CBE=90°,
∴AD⊥CE.
查看更多完整答案,请扫码查看


