《2025年课时训练江苏人民出版社八年级数学上册苏科版》

1. 有两个角____的三角形是等腰三角形(简称“等角对等边”).

答案： 相等

2. 三边都相等的三角形叫作____或____.

答案： 等边三角形　正三角形

3. 等边三角形的性质定理:等边三角形的各角都等于____.

答案： 60°

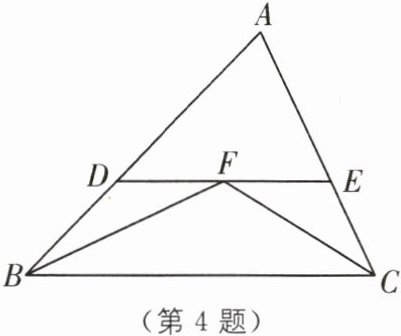
4. (2025·苏州高新区月考)如图,在△ABC中,AB＞AC,∠ABC与∠ACB的平分线交于点F,过点F作DE//BC交AB于点D,交AC于点E,那么下列结论:①DE= BD+CE;②AD= AE;③△ADE的周长= AB+AC;④BF= CF;⑤∠BFC= 90°+ $\frac{∠A}{2}$.其中正确的有( ).


A.①②③
B.①②④
C.①③⑤
D.①③④⑤

答案： C

5. 如图,在△ABC中,ED//BC,∠ABC和∠ACB的平分线分别交ED于点G,F.若FG= 5,ED= 8,则EB+DC的值为____.

答案： 13

6. 新情境 池塘测长 (2025·无锡惠山区期中)如图,在一个池塘旁有一条笔直公路MN,池塘对面有一个建筑A,小明在公路一点B处测得∠ABN= 60°,为了得到他与建筑物A之间的距离,小明沿公路MN继续向东走到点C处,测得∠ACB= 60°,并测得他走了48米,则AB为____米.

答案： 48

7. 提分优练 (2025·山东德州陵城区期中)如图,在△ABC中,AB= BC= AC= 12cm,现有两点M,N分别从点A,B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达点B时,M,N同时停止运动.
(1)点M,N运动几秒时,M,N两点重合?
(2)点M,N运动几秒时,可得到等边三角形AMN?
(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?若存在,请求出此时M,N运动的时间.

答案：
(1)设点M,N运动x秒时,M,N两点重合，
x×1+12=2x,解得x=12.
故点M,N运动12秒时，M,N两点重合。
(2)设点M,N运动t秒时，可得到等边三角形AMN,如图
(1)，
AM=t×1=t,AN=AB−BN=12−2t.
∵三角形AMN是等边三角形,
∴t=12−2t,解得t=4,
∴点M,N运动4秒时，可得到等边三角形AMN.
(3)当点M,N在BC边上运动时，可以得到以MN为底边的等腰三角形，
由
(1)知12秒时M,N两点重合，恰好在C处，
如图
(2)，假设△AMN是等腰三角形，
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB.
∵AB=BC=AC,
∴△ACB是等边三角形，
∴∠C=∠B.
在△ACM和△ABN中，∠AMC=∠ANB，∠C=∠B，AC=AB，
∴△ACM≌△ABN(AAS),
∴CM=BN.
设当点M,N在BC边上运动，M,N运动的时间为y秒时，△AMN是等腰三角形，
∴CM=y−12,NB=36−2y,由CM=NB,得y−12=36−2y,解得y=16.故假设成立.
∴当点M,N在BC边上运动时，能得到以MN为底边的等腰三角形AMN，此时M，N运动的时间为16秒.