《2025年课堂点睛七年级数学上册沪科版》

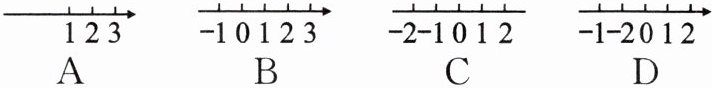
1. 以下是四位同学所画的数轴,其中正确的是(B)

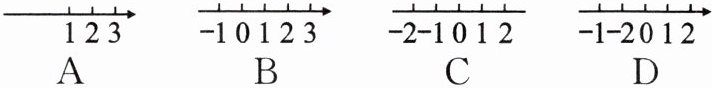
答案： 解：数轴的三要素是原点、正方向和单位长度。
A选项：没有原点，不符合数轴定义。
B选项：具备原点、正方向（向右）和统一的单位长度，符合数轴定义。
C选项：没有正方向，不符合数轴定义。
D选项：单位长度不统一（-1到-2之间距离与其他单位长度不同），不符合数轴定义。
正确的是B。

2. (2024年河南省改编)在下面数轴上,点C表示的数是(-2)

A.3
B.1
C.-2
D.-4

答案： 解：由数轴可知，点C位于原点O左侧，距离原点2个单位长度，所以点C表示的数是-2。
答案：C

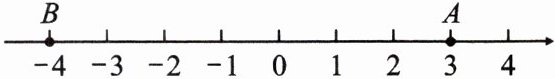
3. 如图,点A表示的数是3；点B表示的数是-4；离原点较近的是点A(选填“A”或“B”)；A,B两点之间有7个单位长度。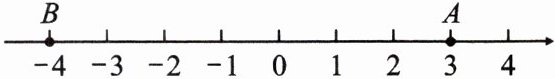

答案： 【解析】：
本题考查数轴上点的位置判断以及数轴上两点间的距离计算。
对于点$A$，其位于数轴上正数部分，且对应刻度为$3$，所以点$A$表示的数是$3$。
对于点$B$，其位于数轴上负数部分，且对应刻度为$- 4$，所以点$B$表示的数是$-4$。
一个数到原点的距离就是它的绝对值，$\vert 3\vert=3$，$\vert -4\vert = 4$，因为$3\lt4$，所以离原点较近的是点$A$。
$A$点表示的数是$3$，$B$点表示的数是$-4$，则$A$、$B$两点之间的距离为：$\vert 3 - (-4)\vert=\vert 3 + 4\vert = 7$，即$A$，$B$两点之间有$7$个单位长度。
【答案】：$3$；$-4$；$A$；$7$。

4. (教材第9页练习第1题变式)如图,指出数轴上的点A,B,C所表示的数,-4,$\frac{3}{2}$,5这三个数分别用点D,E,F在数轴上表示出来。

答案： 解：由数轴可知，点A表示-2.5，点B表示0，点C表示4。
在数轴上表示-4，$\frac{3}{2}$，5：点D在-4处，点E在1.5处，点F在5处。

5. (原创题)数轴上点A到原点的距离是4个单位长度,则点A表示的数为$\pm 4$。

答案： 【解析】：
本题考查数轴的基本概念。在数轴上，一个点到原点的距离表示该点对应的数的绝对值。题目中给出点A到原点的距离是4个单位长度，因此，点A表示的数的绝对值为4。根据绝对值的定义，绝对值为4的数有两个，分别是4和-4。
【答案】：
点A表示的数为$\pm 4$。

数轴上到表示-5的点的距离为2个单位长度的点表示的数为-3或-7。

答案： 解：设该点表示的数为$x$。
根据数轴上两点间距离公式，得$|x - (-5)| = 2$，即$|x + 5| = 2$。
当$x + 5 = 2$时，$x = -3$；
当$x + 5 = -2$时，$x = -7$。
故答案为：$-3$或$-7$。

6. 小明发现一个被墨水污染的数轴(如图),被墨迹盖住部分的整数共有(D)

A.1个
B.2个
C.3个
D.4个

答案： 解：由数轴可知，被墨迹盖住的部分在-3和2之间。
大于-3且小于2的整数有：-2，-1，0，1。
共有4个整数。
答案：D

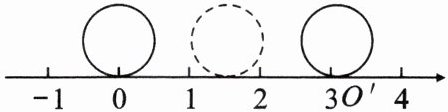
7. (马鞍山博望初中月考卷)如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达$O'$点,点$O'$对应的数是$\pi$。

答案： 【解析】：
本题考查了数轴及圆的周长的计算。
首先，我们知道圆的直径为1个单位长度，那么圆的周长即为圆的直径乘以$\pi$，也就是$\pi × 1 = \pi$。
当圆从原点沿数轴向右滚动一周时，圆上的一点（初始时在原点）会移动到数轴上的某个点，这个点距离原点的距离就是圆的周长，即$\pi$。
由于圆是向右滚动的，所以这一点会到达原点的右侧，并且距离原点$\pi$个单位长度。
因此，点$O'$对应的数就是$\pi$。
【答案】：
$\pi$。

8. (教材第14页习题第7题变式)如图,点A表示的数是-4.(单位长度为1)

(1)在数轴上标出原点；
(2)指出点B所表示的数；
(3)在数轴上找一点C,它与B点的距离为2个单位长度,那么C点表示什么数？

答案：
(1) 解：因为点A表示的数是-4，且点A右侧第4个单位长度处为原点，在数轴上标出原点（图略）。
(2) 解：由原点位置可知，点B在原点右侧第3个单位长度，所以点B表示的数是3。
(3) 解：当点C在点B左侧时，C点表示的数为3 - 2 = 1；当点C在点B右侧时，C点表示的数为3 + 2 = 5。故C点表示的数是1或5。

9. (核心素养·应用意识)刘晓梅从A地出发向东走10m,然后折回向西走3m,又折回向东走6m,问此人此时在A地哪个方向？距离A地多远？

答案： 【解析】：
本题主要考查数轴的应用以及方向和距离的判断。题目描述了一个人在数轴上的移动情况，通过计算他的总移动距离和方向，可以确定他最终的位置。
初始位置在A地，记作0点。
向东走10m，位置变为+10。
折回向西走3m，位置变为$+10 - 3 = +7$。
再折回向东走6m，位置变为$+7 + 6 = +13$。
因此，此人最终在A地的东边13m处。
【答案】：
此人此时在A地的东边，距离A地13m。