第94页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
12. 如图,已知 $ C $ 为 $ AB $ 上一点,$ AC = 15\ cm $,$ CB = \frac{2}{3}AC $。若 $ D $ 为 $ AB $ 的中点,求 $ CD $ 的长。


答案:
12.解:因为$AC=15$ cm,$CB=\frac{2}{3}AC$,所以$CB=\frac{2}{3}×15=10(cm)$,AB=$15+10=25(cm)$.又因为D是AB的中点,所以$AD=\frac{1}{2}AB=12.5$ cm.所以CD=AC - AD=15 - 12.5=2.5(cm).
13.(潍坊安丘市期末)$ C $ 在直线 $ AB $ 上,$ AB = 5 $,$ BC = 2 $,$ C $ 为 $ BD $ 中点,则 $ AD $ 的长为
1或9
。
答案:
13.1或9
14.(潍坊安丘市月考)如图,$ C $ 是线段 $ AB $ 的中点,$ D $ 是线段 $ CB $ 的中点,下列说法错误的是(
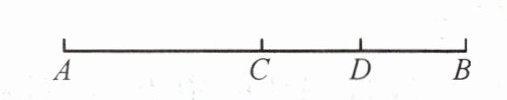
A.$ CD = AC - BD $
B.$ CD = \frac{1}{2}AB - BD $
C.$ AC + BD = BC + CD $
D.$ CD = \frac{1}{3}AB $
D
)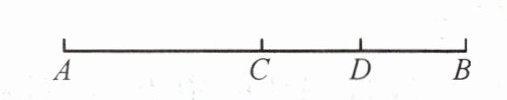
A.$ CD = AC - BD $
B.$ CD = \frac{1}{2}AB - BD $
C.$ AC + BD = BC + CD $
D.$ CD = \frac{1}{3}AB $
答案:
14.D
15.(泰安肥城市期中)在线段 $ AB $ 上取一点 $ C $,使 $ AC = \frac{1}{3}AB $,再在 $ AB $ 的延长线上取一点 $ D $,使 $ DB = \frac{1}{4}AD $,则 $ BC $ 是 $ AD $ 的(
A.$ \frac{1}{3} $
B.$ \frac{2}{3} $
C.$ \frac{1}{2} $
D.$ \frac{3}{2} $
C
)A.$ \frac{1}{3} $
B.$ \frac{2}{3} $
C.$ \frac{1}{2} $
D.$ \frac{3}{2} $
答案:
15.C
16.(凉山州中考)$ C $ 是线段 $ AB $ 的中点,$ D $ 是线段 $ AC $ 的三等分点。若线段 $ AB = 12\ cm $,则线段 $ BD $ 的长为(
A.$ 10\ cm $
B.$ 8\ cm $
C.$ 10\ cm $ 或 $ 8\ cm $
D.$ 2\ cm $ 或 $ 4\ cm $
C
)A.$ 10\ cm $
B.$ 8\ cm $
C.$ 10\ cm $ 或 $ 8\ cm $
D.$ 2\ cm $ 或 $ 4\ cm $
答案:
16.C
17. 如图,将一根绳子对折以后用线段 $ AB $ 表示,现从点 $ C $ 处将绳子剪断,剪断后的各段绳子中最长的一段为 $ 60\ cm $,且 $ AC = \frac{1}{3}BC $,则这条绳子的原长为

80 cm或160 cm
。
答案:
17.80 cm或160 cm
18. 如图,已知 $ B $,$ C $ 两点把线段 $ AD $ 分成 $ 2:4:3 $ 的三部分,$ M $ 是 $ AD $ 的中点,若 $ CD = 6 $,求线段 $ MC $ 的长。
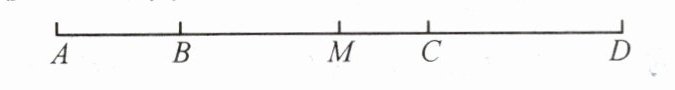
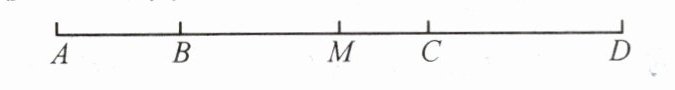
答案:
18.解:因为B,C两点把线段AD分成2:4:3的三部分,所以AB=$\frac{2}{9}AD$,$BC=\frac{4}{9}AD$,$CD=\frac{1}{3}AD$.又因为CD=6,所以AD=18.因为M是AD的中点,所以$MD=\frac{1}{2}AD=9$.所以MC=MD - CD=9 - 6=3.
19.(聊城期中)如图所示,点 $ C $ 在线段 $ AB $ 上,线段 $ AC = 6\ cm $,$ BC = 4\ cm $,点 $ M $,$ N $ 分别是 $ AC $,$ BC $ 的中点。

【问题情境】
(1)求线段 $ MN $ 的长度;
【问题探究】
(2)若点 $ C $ 在线段 $ AB $ 上移动,其他条件不变,根据(1)的计算过程和结果,你能猜测出 $ MN $ 的长度与 $ AB $ 的长度之间的关系吗?请用一句简洁的话表述你发现的规律。
【拓展变式 1】
如图,$ C $ 是线段 $ AB $ 上的点,$ D $ 是线段 $ AC $ 的中点,$ E $ 是线段 $ BC $ 的中点。若 $ DE = 10 $,则 $ AB $ 的长为

【拓展变式 2】
(潍坊期中)已知线段 $ AC $ 和 $ BC $ 在同一直线上,如果 $ AC = 6.6\ cm $,$ BC = 2.4\ cm $,那么线段 $ AC $ 的中点与线段 $ BC $ 的中点之间的距离为

【问题情境】
(1)求线段 $ MN $ 的长度;
【问题探究】
(2)若点 $ C $ 在线段 $ AB $ 上移动,其他条件不变,根据(1)的计算过程和结果,你能猜测出 $ MN $ 的长度与 $ AB $ 的长度之间的关系吗?请用一句简洁的话表述你发现的规律。
【拓展变式 1】
如图,$ C $ 是线段 $ AB $ 上的点,$ D $ 是线段 $ AC $ 的中点,$ E $ 是线段 $ BC $ 的中点。若 $ DE = 10 $,则 $ AB $ 的长为
20
。
【拓展变式 2】
(潍坊期中)已知线段 $ AC $ 和 $ BC $ 在同一直线上,如果 $ AC = 6.6\ cm $,$ BC = 2.4\ cm $,那么线段 $ AC $ 的中点与线段 $ BC $ 的中点之间的距离为
2.1 cm或4.5 cm
。
答案:
19.解:
(1)因为AC=6 cm,BC=4 cm,点M是AC的中点,点N是BC的中点,所以$MC=AM=\frac{1}{2}AC=3$ cm,$CN=BN=\frac{1}{2}BC=2$ cm.所以MN=MC+CN=5 cm.
(2)$MN=\frac{1}{2}AB$.发现的规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
[拓展变式1] 20
[拓展变式2] 2.1 cm或4.5 cm
(1)因为AC=6 cm,BC=4 cm,点M是AC的中点,点N是BC的中点,所以$MC=AM=\frac{1}{2}AC=3$ cm,$CN=BN=\frac{1}{2}BC=2$ cm.所以MN=MC+CN=5 cm.
(2)$MN=\frac{1}{2}AB$.发现的规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
[拓展变式1] 20
[拓展变式2] 2.1 cm或4.5 cm
查看更多完整答案,请扫码查看


