《2025年名校课堂七年级数学上册青岛版》

9. 数轴上点 $ A $ 表示 $ -3 $，$ B,C $ 两点表示的数互为相反数，且点 $ B $ 到点 $ A $ 的距离是 $ 2 $，则点 $ C $ 表示的数是1或5。

答案： 9.1或5

10. 如图，图中数轴的单位长度为 $ 1 $。请回答下列问题：
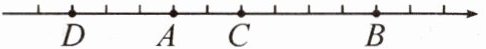
(1) 如果点 $ A,B $ 表示的数互为相反数，那么点 $ C $ 表示的数是多少？
(2) 如果点 $ D,B $ 表示的数互为相反数，那么点 $ C,D $ 表示的数是多少？

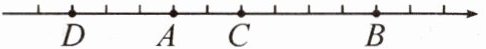
答案： 10.解：
(1)点C表示的数是-1.
(2)点C表示的数是0.5,点D表示的数
是-4.5.

11. 若数 $ a $ 在数轴上的对应点在原点左边，且 $ |a|=\dfrac{1}{2} $，则 $ a $ 的值为- $\frac {1}{2}$。

答案： $11.- \frac {1}{2}$

12. 如图，已知数轴的单位长度为 $ 1 $。如果点 $ A,B $ 表示的数的绝对值相等，那么点 $ A $ 表示的数是(C)


A.$ -4 $
B.$ 0 $
C.$ -2 $
D.$ 4 $

答案： 12.C

13. 如图，四个有理数在数轴上的对应点分别为 $ M,P,N,Q $。若点 $ M,N $ 表示的有理数互为相反数，则图中表示绝对值最大的数的点是(A)


A.点 $ Q $
B.点 $ N $
C.点 $ M $
D.点 $ P $

答案： 13.A

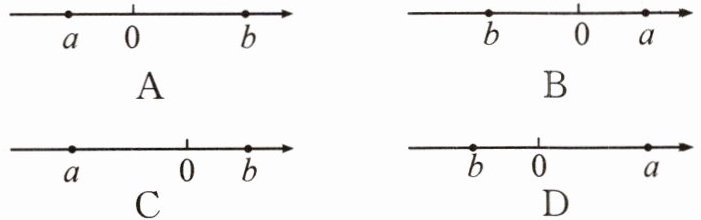
14. 【几何直观】已知 $ a,b $ 是不为 $ 0 $ 的有理数，且 $ |a|=-a,|b|=b,|a|＞|b| $，那么用数轴上的点来表示 $ a,b $ 时，正确的是(C)

答案： 14.C

15. 新考向 推理能力 一只电子虫在一条数轴上，从 $ 0 $ 开始，第 $ 1 $ 次向右跳 $ 1 $ 个单位长度，紧接着第 $ 2 $ 次向左跳 $ 2 $ 个单位长度，第 $ 3 $ 次向右跳 $ 3 $ 个单位长度，第 $ 4 $ 次向左跳 $ 4 $ 个单位长度……依此规律下去，当它跳第 $ 100 $ 次落下时，落点在数轴上表示的数是-50。

答案： 15.-50

16. 【特例分析】
(1) 借助数轴，回答下列问题。
① 从 $ -1 $ 到 $ 1 $ 有 $ 3 $ 个整数，分别是-1,0,1；
② 从 $ -2 $ 到 $ 2 $ 有 $ 5 $ 个整数，分别是-2,-1,0,1,2；
③ 从 $ -3 $ 到 $ 3 $ 有 $ 7 $ 个整数，分别是-3,-2,-1,0,1,2,3；
④ 从 $ -100 $ 到 $ 100 $ 有201个整数；
【深入研究】
(2) 根据以上规律，从 $ -3.9 $ 到 $ 3.9 $ 有7个整数，从 $ -10.1 $ 到 $ 10.1 $ 有21个整数；
【拓展应用】
(3) 在单位长度是 $ 1 cm $ 的数轴上任意画一条长为 $ 1000 cm $ 的线段 $ AB $，线段 $ AB $ 盖住的整点最多有多少个？

答案： 16.解：
(1)①-1,0,1 ②-2,-1,0,1,2 ③-3,-2,-1,0,1,2,3
④201
(2)7 21
(3)①当线段AB的端点在整点时，盖住的整点有
1001个;②当线段AB的端点不在整点，即在两个整点之间时，盖住的
整点有1000个.综上所述，线段AB盖住的整点最多有1001个.