第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
10. 写出绝对值大于 $5$ 且小于 $8$ 的所有整数:
±6,±7
。
答案:
10.±6,±7
11. 下列式子中,正确的是(
A.$-6 > -8$
B.$-11\ 000 > 0$
C.$-15 < -17$
D.$13 < 0.3$
A
)A.$-6 > -8$
B.$-11\ 000 > 0$
C.$-15 < -17$
D.$13 < 0.3$
答案:
11.A
12. 下列说法中,正确的是(
A.有理数中既没有最大的数,也没有最小的数
B.正数没有最大的数,有最小的数
C.负数没有最小的数,有最大的数
D.整数既有最大的数,也有最小的数
A
)A.有理数中既没有最大的数,也没有最小的数
B.正数没有最大的数,有最小的数
C.负数没有最小的数,有最大的数
D.整数既有最大的数,也有最小的数
答案:
12.A
13. 大于 $-4.6$ 而小于 $2.3$ 的整数共有(
A.$7$ 个
B.$6$ 个
C.$5$ 个
D.$4$ 个
A
)A.$7$ 个
B.$6$ 个
C.$5$ 个
D.$4$ 个
答案:
13.A
14. 若有理数 $a$,$b$ 在数轴上对应点的位置如图所示,则下列式子正确的是(

A.$\vert b\vert < \vert a\vert$
B.$\vert a\vert > -b$
C.$b > a$
D.$\vert b\vert > -a$
D
)
A.$\vert b\vert < \vert a\vert$
B.$\vert a\vert > -b$
C.$b > a$
D.$\vert b\vert > -a$
答案:
14.D
15. 在 $-0.142\ 6$ 中用数字 $3$ 替换其中的一个非零数字后,使所得的数最大,则被替换的数字是(
A.$1$
B.$2$
C.$4$
D.$6$
C
)A.$1$
B.$2$
C.$4$
D.$6$
答案:
15.C
16. (聊城阳谷县期中)比较下列各对数的大小:
$-(+0.3)$
$-(+0.3)$
>
$-\vert -\dfrac{1}{3}\vert$。(填“$>$”“$=$”或“$<$”)
答案:
16.>
17. 新考向 新定义问题 若 $[x]$ 表示小于 $x$ 的最大整数,如:$[-2.3]=-3$,$[4]=3$,则:
(1)$[5\dfrac{1}{2}]=$
(2)$[-3]=$
(3)$[-8\dfrac{1}{3}]=$
(1)$[5\dfrac{1}{2}]=$
5
;(2)$[-3]=$
-4
;(3)$[-8\dfrac{1}{3}]=$
-9
。
答案:
17.
(1)5
(2)-4
(3)-9
(1)5
(2)-4
(3)-9
18. 已知在数轴上有 $A$,$B$,$C$ 三个点,点 $A$ 表示的数是 $-4$,点 $B$ 表示绝对值最小的数,点 $C$ 表示的数是最大的负整数。
(1)在数轴上把 $A$,$B$,$C$ 三点表示出来,并比较这三个点表示的数的大小(用“$<$”连接);
(2)直接写出如何移动点 $C$,可以使它到点 $A$ 和点 $B$ 的距离相等。
(1)在数轴上把 $A$,$B$,$C$ 三点表示出来,并比较这三个点表示的数的大小(用“$<$”连接);
(2)直接写出如何移动点 $C$,可以使它到点 $A$ 和点 $B$ 的距离相等。
答案:
18.解:
(1)因为点 B 表示绝对值最小的数,点 C 表示的数是最大的负整数,所以点 B 表示的数是 0,点 C 表示的数是-1.A,B,C 三点在数轴上表示如图所示:
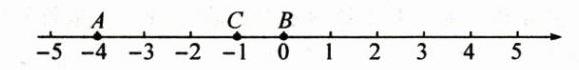
根据“数轴上左边的数小于右边的数”可知,-4< -1<0.
(2)将点 C 向左移动 1 个单位长度,可以使它到点 A 和点 B 的距离相等.
18.解:
(1)因为点 B 表示绝对值最小的数,点 C 表示的数是最大的负整数,所以点 B 表示的数是 0,点 C 表示的数是-1.A,B,C 三点在数轴上表示如图所示:
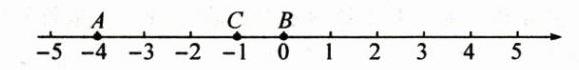
根据“数轴上左边的数小于右边的数”可知,-4< -1<0.
(2)将点 C 向左移动 1 个单位长度,可以使它到点 A 和点 B 的距离相等.
19. 【数形结合思想】有理数 $a$,$b$,$c$ 在数轴上对应点的位置如图所示。

(1)用“$<$”“$>$”或“$=$”填空:$a$
(2)利用数轴化简:
① $\vert a\vert =$
② $\vert b\vert =$
③ $\vert c\vert =$
④ $\vert -a\vert =$
⑤ $\vert -b\vert =$
⑥ $\vert -c\vert =$
(3)试将 $a$,$b$,$c$,$-a$,$-b$,$-c$,$0$ 用“$<$”连接起来。

(1)用“$<$”“$>$”或“$=$”填空:$a$
<
$0$,$b$<
$0$,$c$>
$0$;(2)利用数轴化简:
① $\vert a\vert =$
-a
;② $\vert b\vert =$
-b
;③ $\vert c\vert =$
c
;④ $\vert -a\vert =$
-a
;⑤ $\vert -b\vert =$
-b
;⑥ $\vert -c\vert =$
c
;(3)试将 $a$,$b$,$c$,$-a$,$-b$,$-c$,$0$ 用“$<$”连接起来。
答案:
19.解:
(1)< < >
(2)①-a ②-b ③c ④-a ⑤-b ⑥c
(3)b<a<-c<0<c<-a<-b.
(1)< < >
(2)①-a ②-b ③c ④-a ⑤-b ⑥c
(3)b<a<-c<0<c<-a<-b.
查看更多完整答案,请扫码查看


