《2025年全效学习九年级科学全一册浙教版》

7. 图甲是一款家用电热器,旋钮开关位置如图乙所示有三种:关闭、低温挡($400W$)和高温挡($800W$)。电热器内部有两根电热丝$R_{1}和R_{2}$,小明绘制了简易原理图如图丙所示。

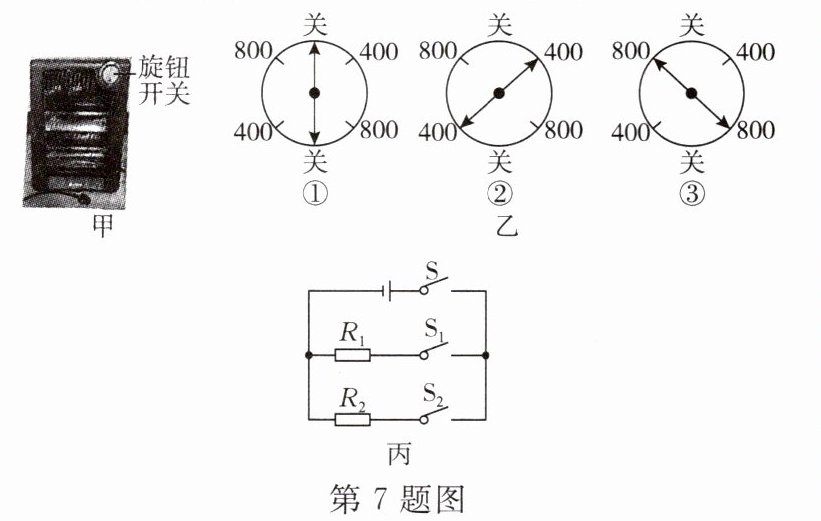
(1)电热器的工作原理是通过电流做功将电能转化为____。
(2)在图丙上闭合开关$S_{1}$、$S_{2}和S$,相当于电热器旋钮开关位于图乙中的____(选填“①”“②”或“③”)。
(3)为了比较高温挡和空调的功率大小,小明测出空调$4h耗电量为3.6kW\cdot h$,其功率为____。

答案： 7.
(1)内能
(2)③
(3)900W

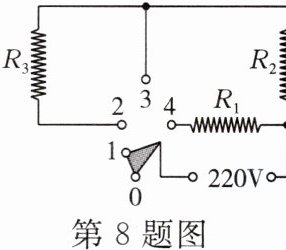
8. 火锅是人们比较喜欢的一种饮食方式,如图所示为小柯家使用的一款电火锅工作电路原理图,它有高、中、低三个加热挡位,旋钮开关可以分别置于“$0和1$”“$1和2$”“$2和3$”或“$3和4$”接线柱。正常工作时,低温挡功率为高温挡功率的$\frac{1}{5}$,$R_{1}的阻值为242Ω$,$R_{2}的阻值为60.5Ω$(忽略温度对电阻的影响)。
(1)请指出开关置于什么接线柱时,火锅处于低温挡。
(2)$R_{3}$的阻值是多少欧姆? 电火锅处于低温挡正常工作时,在$1min$内产生的热量是多少焦耳?

答案：
(1)当旋钮开关置于“1和2”接线柱时,$R_2$、$R_3$串联,电路中电阻最大,根据$P=\frac{U^2}{R}$可知,电功率最小,电火锅处于低温挡。
(2)当旋钮开关置于“2和3”接线柱时,$R_3$短路,电路为$R_2$的简单电路,电路电阻较大,根据$P=\frac{U^2}{R}$可知,电功率较大,电火锅处于中温挡；
当旋钮开关置于“3和4”接线柱时,$R_1$、$R_2$并联,电路中电阻最小,根据$P=\frac{U^2}{R}$可知,电功率最大,电火锅处于高温挡；
高温挡时的电功率:$P_{高}=P_1+P_2=\frac{U^2}{R_1}+\frac{U^2}{R_2}=\frac{(220V)^2}{242\Omega}+\frac{(220V)^2}{60.5\Omega}=1000W$,
由题意知,低温挡功率为高温挡功率的$\frac{1}{5}$,即$P_{低}=\frac{1}{5}P_{高}=\frac{1}{5}×1000W=200W$,由$P=\frac{U^2}{R}$可得,低温挡时电路的总电阻$R_{总}=\frac{U^2}{P_{低}}=\frac{(220V)^2}{200W}=242\Omega$,因串联电路中总电阻等于各分电阻之和,所以$R_3=R_{总}-R_2=242\Omega-60.5\Omega=181.5\Omega$。
电火锅处于低温挡正常工作时,在1min内产生的热量$Q=W=P_{低}t=200W×60s=1.2×10^4J$。

9. 如图甲所示的多功能养生壶具有精细烹饪、营养量化等功能,深受市场认可和欢迎。如图乙所示是某品牌养生壶简化电路图,该养生壶铭牌上的部分参数如表所示。$[ρ_{水}= 1×10^{3}kg/m^{3},c_{水}= 4.2×10^{3}J/(kg\cdot ^{\circ}C),g= 10N/kg]$。

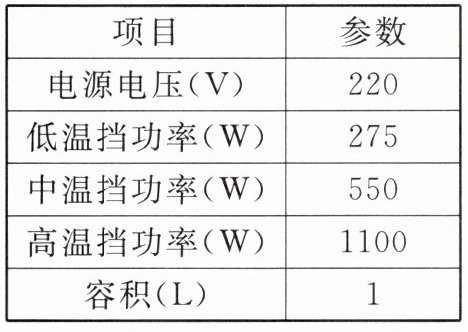
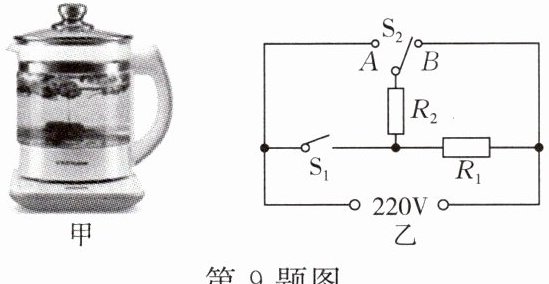
(1)开关$S_{1}$、$S_{2}$处于什么状态,养生壶为高温挡,说明判断依据。
(2)求$R_{1}$的阻值。
(3)养生壶处于低温挡工作时,求电路中的电流大小。
(4)在标准大气压下,使用高温挡将初温是$12^{\circ}C$的一壶水烧开,若养生壶高温挡加热效率为$80\%$,求水吸收的热量和烧开一壶水需要的时间。

答案：
(1)当开关$S_1$闭合,$S_2$接B时,养生壶为高温挡。因为当开关$S_1$闭合,$S_2$接B时,电阻$R_1$、$R_2$并联,电路中的总电阻最小,总功率最大,所以此状态为高温挡。
(2)当$S_1$闭合,$S_2$接A时,只有电阻$R_1$接入电路,养生壶处于中温挡。由$P=UI$得,正常工作时通过$R_1$的电流为$I_1=\frac{P_1}{U}=\frac{550W}{220V}=2.5A$,由$I=\frac{U}{R}$得,$R_1$的阻值为$R_1=\frac{U}{I_1}=\frac{220V}{2.5A}=88\Omega$。
(3)当$S_1$断开,$S_2$接A时,养生壶处于低温挡。由$P=UI$得,养生壶在低温挡工作时电路中的电流为$I_{低}=\frac{P_{低}}{U}=\frac{275W}{220V}=1.25A$。
(4)水的质量$m=\rho V=1×10^3kg/m^3×1×10^{-3}m^3=1kg$,水吸收的热量$Q_{吸}=cm(t-t_0)=4.2×10^3J/(kg\cdot^{\circ}C)×1kg×(100^{\circ}C-12^{\circ}C)=3.696×10^5J$。由$\eta=\frac{Q_{吸}}{W}$,$W=Pt$得,烧开一壶水需要的时间为$t=\frac{Q_{吸}}{P_{高}×\eta}=\frac{3.696×10^5J}{1100W×80\%}=420s=7min$。