《2025年暑假生活指导八年级合订本青岛出版社》

1. 已知一个正方形的面积是$4a^{2} + 12ab + 9b^{2}$,其中$a$,$b$为正数,则此正方形的边长是______.

答案： $2a + 3b$

2. 在一个钝角三角形中,已知一个锐角为$30^{\circ}$,则另一个锐角$\alpha$的取值范围是______.

答案： $0^{\circ} ＜ \alpha ＜ 60^{\circ}$

3. 在$\triangle ABC$中,若$\angle A = 70^{\circ}$,$\angle B与\angle C的平分线相交于点E$,则$\angle BEC = $______.

答案： 125°

4. 下列各式中,属于完全平方式的有( )个.
①$x^{2} + 2xy + y^{2}$
②$\frac{1}{9}m^{2} - 2mn + 9n^{2}$
③$-4a^{2} - 4ab - 4b^{2}$
④$a^{2} + 2ab - b^{2}$
⑤$m^{2} + \frac{1}{m^{2}} - 2$
⑥$25x^{2} - 10xy + y^{2}$

A.5
B.4
C.3
D.2

答案： 1. 首先明确完全平方公式：
完全平方公式为$(a\pm b)^{2}=a^{2}\pm 2ab + b^{2}$。
2. 然后对各式进行分析：
①$x^{2}+2xy + y^{2}$：
因为$x^{2}+2xy + y^{2}=(x + y)^{2}$，符合完全平方公式$(a + b)^{2}=a^{2}+2ab + b^{2}$（这里$a = x$，$b = y$），所以是完全平方式。
②$\frac{1}{9}m^{2}-2mn + 9n^{2}$：
由于$\frac{1}{9}m^{2}-2mn + 9n^{2}=(\frac{1}{3}m)^{2}-2mn+(3n)^{2}$，而$(\frac{1}{3}m - 3n)^{2}=(\frac{1}{3}m)^{2}-2×\frac{1}{3}m×3n+(3n)^{2}=\frac{1}{9}m^{2}-2mn + 9n^{2}$，符合完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}$（这里$a=\frac{1}{3}m$，$b = 3n$），所以是完全平方式。
③$-4a^{2}-4ab - 4b^{2}$：
提取$-4$得$-4(a^{2}+ab + b^{2})$，$a^{2}+ab + b^{2}$不符合$a^{2}\pm 2ab + b^{2}$的形式，所以$-4a^{2}-4ab - 4b^{2}$不是完全平方式。
④$a^{2}+2ab - b^{2}$：
不符合$a^{2}\pm 2ab + b^{2}$的形式（后面是$-b^{2}$，应为$+b^{2}$），所以不是完全平方式。
⑤$m^{2}+\frac{1}{m^{2}}-2$：
因为$m^{2}+\frac{1}{m^{2}}-2=(m-\frac{1}{m})^{2}$，符合完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}$（这里$a = m$，$b=\frac{1}{m}$），所以是完全平方式。
⑥$25x^{2}-10xy + y^{2}$：
因为$25x^{2}-10xy + y^{2}=(5x)^{2}-2×5x× y + y^{2}=(5x - y)^{2}$，符合完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}$（这里$a = 5x$，$b = y$），所以是完全平方式。
3. 最后统计完全平方式的个数：
①②⑤⑥是完全平方式，共$4$个。
所以答案是B。

5. 若$n$为任意整数,$(n + 11)^{2} - n^{2}的值可以被k$整除,则$k$为( ).

A.11
B.22
C.11或22
D.11的倍数

答案： 1. 首先，利用平方差公式$a^{2}-b^{2}=(a + b)(a - b)$对$(n + 11)^{2}-n^{2}$进行化简：
对于$(n + 11)^{2}-n^{2}$，这里$a=n + 11$，$b = n$。
根据平方差公式$(n + 11)^{2}-n^{2}=[(n + 11)+n][(n + 11)-n]$。
2. 然后，进行计算：
先计算$[(n + 11)+n][(n + 11)-n]$，$(n + 11)+n=2n + 11$，$(n + 11)-n = 11$。
所以$(n + 11)^{2}-n^{2}=(2n + 11)×11$。
因为$n$为任意整数，$(n + 11)^{2}-n^{2}=11(2n + 11)$，所以$(n + 11)^{2}-n^{2}$能被$11$整除，$k = 11$。
故答案是A。

6. 如图,$AB// CD$,则$\angle 1与\angle 2 + \angle 3$的关系是( ).


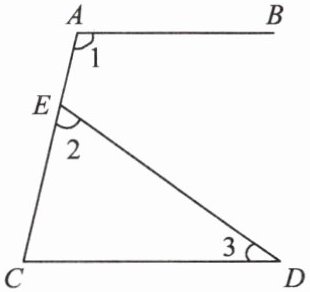
A.$\angle 1 ＞ \angle 2 + \angle 3$
B.$\angle 1 = \angle 2 + \angle 3$
C.$\angle 1 + \angle 2 + \angle 3 = 180^{\circ}$
D.$\angle 1 ＜ \angle 2 + \angle 3$

答案： B