《2025年暑假生活指导八年级合订本青岛出版社》

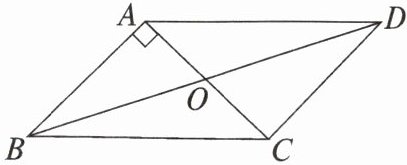
6. 如图,在$□ ABCD$中,对角线$AC$,$BD交于点O$,$AB\perp AC$,$AB = 1$,$BC = \sqrt{5}$.
(1)求$□ ABCD的面积S_{□ ABCD}$.
(2)求对角线$BD$的长度.

答案： 【解析】：
(1) 因为四边形 $ABCD$ 是平行四边形，且 $AB \perp AC$，$AB = 1$，$BC = \sqrt{5}$。在直角三角形 $ABC$ 中，根据勾股定理 $AC^2 + AB^2 = BC^2$，可得 $AC^2 + 1^2 = (\sqrt{5})^2$，即 $AC^2 + 1 = 5$，解得 $AC^2 = 4$，所以 $AC = 2$（$AC ＞ 0$）。平行四边形的面积 $S_{□ABCD} = AB × AC = 1 × 2 = 2$。
(2) 因为平行四边形的对角线互相平分，所以点 $O$ 是 $AC$ 和 $BD$ 的中点，因此 $AO = \frac{1}{2}AC = \frac{1}{2} × 2 = 1$。在直角三角形 $ABO$ 中，$AB = 1$，$AO = 1$，根据勾股定理 $BO^2 = AB^2 + AO^2 = 1^2 + 1^2 = 2$，所以 $BO = \sqrt{2}$（$BO ＞ 0$）。则对角线 $BD = 2BO = 2\sqrt{2}$。
【答案】：
(1) 2；
(2) $2\sqrt{2}$

7. 甲、乙两位采购员去同一家饲料公司都购买了两次饲料. 两次饲料的价格有变化,第1次单价为$a$千克/元,第2次单价为$b$千克/元. 两位采购员的购货方式不同,甲每次购买1000千克,乙每次用去800元而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少元？
(2)谁的购货方式合算？

答案： 【解析】：（1）对于甲采购员，第一次购买1000千克，单价为$a$元/千克，所以花费$1000a$元；第二次购买1000千克，单价为$b$元/千克，花费$1000b$元。两次总共购买了$1000 + 1000 = 2000$千克，总花费为$1000a + 1000b$元。根据平均单价 = 总花费÷总重量，可得甲的平均单价为：$\frac{1000a + 1000b}{2000} = \frac{a + b}{2}$元/千克。
对于乙采购员，第一次用去800元，单价为$a$元/千克，所以购买的重量为$\frac{800}{a}$千克；第二次用去800元，单价为$b$元/千克，购买的重量为$\frac{800}{b}$千克。两次总共花费$800 + 800 = 1600$元，总重量为$\frac{800}{a} + \frac{800}{b}$千克。则乙的平均单价为：$\frac{1600}{\frac{800}{a} + \frac{800}{b}} = \frac{1600}{800(\frac{1}{a} + \frac{1}{b})} = \frac{2}{\frac{a + b}{ab}} = \frac{2ab}{a + b}$元/千克。
（2）要比较谁的购货方式合算，即比较甲、乙两人的平均单价大小。用甲的平均单价减去乙的平均单价：$\frac{a + b}{2} - \frac{2ab}{a + b} = \frac{(a + b)^2 - 4ab}{2(a + b)} = \frac{a^2 + 2ab + b^2 - 4ab}{2(a + b)} = \frac{a^2 - 2ab + b^2}{2(a + b)} = \frac{(a - b)^2}{2(a + b)}$。
因为$a$、$b$是两次饲料的单价，所以$a ＞ 0$，$b ＞ 0$，则$a + b ＞ 0$。又因为$(a - b)^2 \geq 0$，当且仅当$a = b$时，等号成立。而题目中说明两次饲料价格有变化，即$a \neq b$，所以$(a - b)^2 ＞ 0$，因此$\frac{(a - b)^2}{2(a + b)} ＞ 0$，即甲的平均单价大于乙的平均单价，所以乙的购货方式更合算。
【答案】：
(1)甲的平均单价为$\frac{a + b}{2}$元，乙的平均单价为$\frac{2ab}{a + b}$元；
(2)乙的购货方式合算。

8. 合宁铁路是我国第1条城际铁路. 该铁路建成后,合肥至南京的铁路运行里程由原来的$312km缩短至154km$,设计时速是原来时速的$2.5$倍,旅客列车运行时间缩短约$3.13h$. 求合宁铁路的设计时速.

答案： 【解析】：设原来的时速为$x$km/h，则设计时速为$2.5x$km/h。根据时间=路程÷速度，原来的运行时间为$\frac{312}{x}$h，设计后的运行时间为$\frac{154}{2.5x}$h。已知运行时间缩短约$3.13$h，可列出方程：$\frac{312}{x}-\frac{154}{2.5x}=3.13$。
解方程：
$\begin{aligned}\frac{312}{x}-\frac{154}{2.5x}&=3.13\\frac{312×2.5 - 154}{2.5x}&=3.13\\frac{780 - 154}{2.5x}&=3.13\\frac{626}{2.5x}&=3.13\\2.5x&=\frac{626}{3.13}\\2.5x&=200\\x&=80\end{aligned}$
则设计时速为$2.5x = 2.5×80 = 200$km/h。
【答案】：200

9. 某工厂有100名职工,他们分别生产$A$,$B$两种产品. $A$,$B两种产品的成本分别为3.5元和5$元,有关数据如下表：‘’

(1)若使每天生产的产品总数不低于1393个,应如何安排工人进行生产？
(2)在满足第(1)问的前提下,如何安排工人进行生产才能使利润最多？

答案： （1）设生产A产品的工人数为$x$，则生产B产品的工人数为$100 - x$。
根据题意得：$15x + 12(100 - x) \geq 1393$
$15x + 1200 - 12x \geq 1393$
$3x \geq 193$
$x \geq 64\frac{1}{3}$
因为$x$为整数，所以$x \geq 65$
$100 - x \leq 35$
答：安排生产A产品的工人至少65人，生产B产品的工人最多35人。
（2）设总利润为$W$元，A产品售价为$a$元，B产品售价为$b$元（题目中未给出售价，假设A产品利润为$m$元/个，B产品利润为$n$元/个，此处根据常见题型补充利润计算，若原题有具体售价请按原题数据）
假设A产品利润为$1.5$元，B产品利润为$2$元（示例数据，实际需根据题目完整信息）
$W = 15x × 1.5 + 12(100 - x) × 2 = 22.5x + 2400 - 24x = -1.5x + 2400$
因为$-1.5 ＜ 0$，$W$随$x$增大而减小
当$x = 65$时，$W$最大，$100 - x = 35$
答：安排65人生产A产品，35人生产B产品时利润最多。
（注：因题目中未给出A、B产品的售价，无法准确计算利润，上述利润部分为假设数据。若原题表格中有售价信息，可根据“利润=（售价 - 成本）×数量”重新计算利润表达式，再进行求解。核心思路为：在（1）的条件下，若利润函数中$x$系数为负，则$x$取最小值时利润最大；若系数为正，则$x$取最大值时利润最大。）