《2025年暑假生活指导八年级合订本青岛出版社》

10. 把下列各式分解因式.
(1)$4x^{2} - 4xy + y^{2} - z^{2}$
(2)$25(a + b)^{2} - 16(a - b)^{2}$
(3)$-x + 2x^{2} - x^{3}$
(4)$(y + 1)(y + 2) + \frac{1}{4}$

答案： 【解析】：
(1) 先将前三项利用完全平方公式分解，得到$(2x - y)^2 - z^2$，再利用平方差公式分解为$(2x - y + z)(2x - y - z)$。
(2) 把$25(a + b)^2$看作$[5(a + b)]^2$，$16(a - b)^2$看作$[4(a - b)]^2$，利用平方差公式分解为$[5(a + b) + 4(a - b)][5(a + b) - 4(a - b)]$，化简后得到$(9a + b)(a + 9b)$。
(3) 先提取公因式$-x$，得到$-x(1 - 2x + x^2)$，括号内利用完全平方公式分解为$-x(x - 1)^2$。
(4) 先展开$(y + 1)(y + 2)$得$y^2 + 3y + 2$，再加上$\frac{1}{4}$得到$y^2 + 3y + \frac{9}{4}$，最后利用完全平方公式分解为$(y + \frac{3}{2})^2$。
【答案】：
(1)$(2x - y + z)(2x - y - z)$；
(2)$(9a + b)(a + 9b)$；
(3)$-x(x - 1)^2$；
(4)$(y + \frac{3}{2})^2$

11. 解下列不等式或不等式组,并将解集表示在数轴上.
(1)$\frac{x - 5}{2} ＞ x - 4$
(2)$-\frac{x}{3} + \frac{x}{15}\leqslant - 1$
(3)$\begin{cases}x - 5\geqslant 2x - 1,\\3x - 2\leqslant 4 - \frac{3}{2}x\end{cases} $

答案： 【解析】：
(1) 解不等式$\frac{x - 5}{2} ＞ x - 4$，
两边同时乘以 2 得：$x - 5 ＞ 2(x - 4)$，
去括号：$x - 5 ＞ 2x - 8$，
移项：$x - 2x ＞ -8 + 5$，
合并同类项：$-x ＞ -3$，
系数化为 1：$x ＜ 3$。
(2) 解不等式$-\frac{x}{3} + \frac{x}{15}\leqslant - 1$，
通分，两边同时乘以 15 得：$-5x + x \leqslant -15$，
合并同类项：$-4x \leqslant -15$，
系数化为 1：$x \geqslant \frac{15}{4}$。
(3) 解不等式组$\begin{cases}x - 5\geqslant 2x - 1 \\3x - 2\leqslant 4 - \frac{3}{2}x\end{cases}$，
解第一个不等式：$x - 5\geqslant 2x - 1$，
移项：$x - 2x \geqslant -1 + 5$，
合并同类项：$-x \geqslant 4$，
系数化为 1：$x \leqslant -4$。
解第二个不等式：$3x - 2\leqslant 4 - \frac{3}{2}x$，
两边同时乘以 2 得：$6x - 4 \leqslant 8 - 3x$，
移项：$6x + 3x \leqslant 8 + 4$，
合并同类项：$9x \leqslant 12$，
系数化为 1：$x \leqslant \frac{4}{3}$。
所以不等式组的解集为$x \leqslant -4$。
【答案】：
(1)$x ＜ 3$；
(2)$x \geqslant \frac{15}{4}$；
(3)$x \leqslant -4$

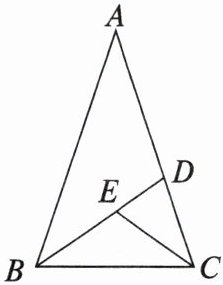
12. 如图,在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,$BD$,$CE分别是\angle ABC$,$\angle BCD$的平分线.
(1)求$\angle DEC$的度数.
(2)直接写出图中所有的等腰三角形.

答案： 【解析】：
(1)在$\triangle ABC$中，$AB = AC$，$\angle A = 36^{\circ}$，所以$\angle ABC=\angle ACB=\frac{180^{\circ}-36^{\circ}}{2}=72^{\circ}$。
因为$BD$是$\angle ABC$的平分线，所以$\angle ABD=\angle DBC=\frac{72^{\circ}}{2}=36^{\circ}$。
在$\triangle ABD$中，$\angle A = 36^{\circ}$，$\angle ABD = 36^{\circ}$，所以$\angle ADB=180^{\circ}-36^{\circ}-36^{\circ}=108^{\circ}$，则$\angle BDC=180^{\circ}-108^{\circ}=72^{\circ}$。
在$\triangle BDC$中，$\angle DBC = 36^{\circ}$，$\angle BDC = 72^{\circ}$，所以$\angle BCD=180^{\circ}-36^{\circ}-72^{\circ}=72^{\circ}$，故$BC = BD$。
因为$CE$是$\angle BCD$的平分线，所以$\angle BCE=\angle ECD=\frac{72^{\circ}}{2}=36^{\circ}$。
在$\triangle BEC$中，$\angle EBC = 36^{\circ}$，$\angle BCE = 36^{\circ}$，所以$\angle BEC=180^{\circ}-36^{\circ}-36^{\circ}=108^{\circ}$，则$\angle DEC=180^{\circ}-\angle BEC=180^{\circ}-108^{\circ}=72^{\circ}$。
(2)由上述计算及角的关系可得：
$\triangle ABC$：$AB = AC$，是等腰三角形。
$\triangle ABD$：$\angle A=\angle ABD = 36^{\circ}$，$AD = BD$，是等腰三角形。
$\triangle BDC$：$\angle BCD=\angle BDC = 72^{\circ}$，$BC = BD$，是等腰三角形。
$\triangle BEC$：$\angle EBC=\angle BCE = 36^{\circ}$，$BE = CE$，是等腰三角形。
$\triangle DEC$：$\angle DEC=\angle ECD = 72^{\circ}$，$DE = DC$，是等腰三角形。
【答案】：
(1)$72^{\circ}$；
(2)$\triangle ABC$，$\triangle ABD$，$\triangle BDC$，$\triangle BEC$，$\triangle DEC$

13. 已知甲正方形的周长比乙正方形的周长长$56m$,它们的面积相差$560m^{2}$,求这两个正方形的边长.

答案： 【解析】：设甲正方形的边长为 $ x $ 米，乙正方形的边长为 $ y $ 米。
根据甲正方形的周长比乙正方形的周长长 $ 56 \, \text{m} $，可得：
$ 4x - 4y = 56 $，化简为 $ x - y = 14 $ ①
根据它们的面积相差 $ 560 \, \text{m}^2 $，可得：
$ x^2 - y^2 = 560 $
利用平方差公式分解得：$ (x - y)(x + y) = 560 $ ②
将①代入②得：$ 14(x + y) = 560 $，解得 $ x + y = 40 $ ③
联立①和③：
$ \begin{cases} x - y = 14 \\ x + y = 40 \end{cases} $
两式相加得 $ 2x = 54 $，解得 $ x = 27 $
将 $ x = 27 $ 代入③得 $ 27 + y = 40 $，解得 $ y = 13 $
【答案】：甲正方形边长为27m，乙正方形边长为13m