第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
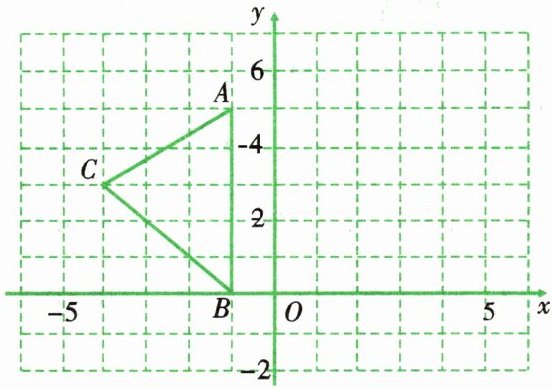
2. 如图,在平面直角坐标系$xOy$中,已知$A(-1,5)$,$B(-1,0)$,$C(-4,3)$.
(1)求出$\triangle ABC$的面积;
(2)在图中作出$\triangle ABC$关于$y$轴的对称图形$\triangle A_1B_1C_1$;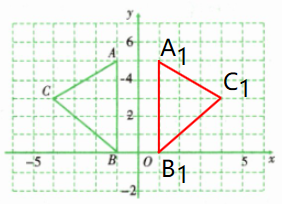
(3)写出点$A_1$,$B_1$,$C_1$的坐标.
(1)求出$\triangle ABC$的面积;
$\frac{15}{2}$
(2)在图中作出$\triangle ABC$关于$y$轴的对称图形$\triangle A_1B_1C_1$;

(3)写出点$A_1$,$B_1$,$C_1$的坐标.
$A_1(1,5),B_1(1,0),C_1(4,3)$

答案:
(1) $\frac{15}{2}$
(2)
(3) $A_1(1,5),B_1(1,0),C_1(4,3)$
(1) $\frac{15}{2}$
(2)

(3) $A_1(1,5),B_1(1,0),C_1(4,3)$
1. (四川乐山最新中考题)点$P(-1,2)$所在象限是(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
B
2. (贵州铜仁最新中考题)如图,在矩形$ABCD$中,$A(-3,2)$,$B(3,2)$,$C(3,-1)$,则$D$的坐标为(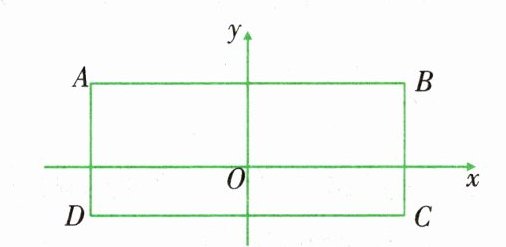
A.$(-2,-1)$
B.$(4,-1)$
C.$(-3,-2)$
D.$(-3,-1)$
D
)
A.$(-2,-1)$
B.$(4,-1)$
C.$(-3,-2)$
D.$(-3,-1)$
答案:
D
“珍宝岛”游戏
在珍宝岛上有一个山洞,船长弗林特在山洞里藏着自己的珍宝.山洞的入口被巧妙地遮掩着,只有老海盗班刚才能找到它.班刚在死之前决定给子孙留一封数字信,说明进入藏宝地的路径和藏宝的地方.
由于老海盗接受过较好的教育,他决定采用坐标法.他取了珍宝岛的地图,在其上画了坐标轴,选了一个单位长度.总之,他做了一切应该做的(如图).作为主要定向标记,他指出四棵橡树的坐标分别是:$(3,5)$,$(-2,7)$,$(-3,4)$,$(3,1)$.宝藏位于连接第一与第三棵橡树的直线和连接第二与第四棵橡树的直线的交点上.
你能找到宝藏的具体位置吗?
在珍宝岛上有一个山洞,船长弗林特在山洞里藏着自己的珍宝.山洞的入口被巧妙地遮掩着,只有老海盗班刚才能找到它.班刚在死之前决定给子孙留一封数字信,说明进入藏宝地的路径和藏宝的地方.
由于老海盗接受过较好的教育,他决定采用坐标法.他取了珍宝岛的地图,在其上画了坐标轴,选了一个单位长度.总之,他做了一切应该做的(如图).作为主要定向标记,他指出四棵橡树的坐标分别是:$(3,5)$,$(-2,7)$,$(-3,4)$,$(3,1)$.宝藏位于连接第一与第三棵橡树的直线和连接第二与第四棵橡树的直线的交点上.
你能找到宝藏的具体位置吗?
$(\frac{3}{41},\frac{185}{41})$
答案:
【解析】:
1. 首先求连接第一棵橡树$(3,5)$与第三棵橡树$(-3,4)$的直线方程:
设直线方程为$y = k_1x + b_1$,将$(3,5)$,$(-3,4)$代入可得:
$\begin{cases}5 = 3k_1 + b_1\\4=-3k_1 + b_1\end{cases}$
两式相减消去$b_1$:$5 - 4=(3k_1 + b_1)-(-3k_1 + b_1)$,即$1 = 6k_1$,解得$k_1=\frac{1}{6}$。
把$k_1=\frac{1}{6}$代入$5 = 3k_1 + b_1$,得$5 = 3×\frac{1}{6}+b_1$,$b_1=\frac{9}{2}$。
所以直线方程为$y=\frac{1}{6}x+\frac{9}{2}$。
2. 然后求连接第二棵橡树$(-2,7)$与第四棵橡树$(3,1)$的直线方程:
设直线方程为$y = k_2x + b_2$,将$(-2,7)$,$(3,1)$代入可得:
$\begin{cases}7=-2k_2 + b_2\\1 = 3k_2 + b_2\end{cases}$
两式相减消去$b_2$:$7 - 1=(-2k_2 + b_2)-(3k_2 + b_2)$,即$6=-5k_2$,解得$k_2=-\frac{6}{5}$。
把$k_2 = -\frac{6}{5}$代入$1 = 3k_2 + b_2$,得$1 = 3×(-\frac{6}{5})+b_2$,$b_2=\frac{23}{5}$。
所以直线方程为$y = -\frac{6}{5}x+\frac{23}{5}$。
3. 最后求两直线交点:
联立$\begin{cases}y=\frac{1}{6}x+\frac{9}{2}\\y = -\frac{6}{5}x+\frac{23}{5}\end{cases}$
即$\frac{1}{6}x+\frac{9}{2}=-\frac{6}{5}x+\frac{23}{5}$
通分:$\frac{5x}{30}+\frac{135}{30}=-\frac{36x}{30}+\frac{138}{30}$
移项:$\frac{5x + 36x}{30}=\frac{138 - 135}{30}$
$41x = 3$,$x=\frac{3}{41}$。
把$x=\frac{3}{41}$代入$y=\frac{1}{6}x+\frac{9}{2}$,$y=\frac{1}{6}×\frac{3}{41}+\frac{9}{2}=\frac{1}{82}+\frac{369}{82}=\frac{370}{82}=\frac{185}{41}$。
【答案】:$(\frac{3}{41},\frac{185}{41})$
1. 首先求连接第一棵橡树$(3,5)$与第三棵橡树$(-3,4)$的直线方程:
设直线方程为$y = k_1x + b_1$,将$(3,5)$,$(-3,4)$代入可得:
$\begin{cases}5 = 3k_1 + b_1\\4=-3k_1 + b_1\end{cases}$
两式相减消去$b_1$:$5 - 4=(3k_1 + b_1)-(-3k_1 + b_1)$,即$1 = 6k_1$,解得$k_1=\frac{1}{6}$。
把$k_1=\frac{1}{6}$代入$5 = 3k_1 + b_1$,得$5 = 3×\frac{1}{6}+b_1$,$b_1=\frac{9}{2}$。
所以直线方程为$y=\frac{1}{6}x+\frac{9}{2}$。
2. 然后求连接第二棵橡树$(-2,7)$与第四棵橡树$(3,1)$的直线方程:
设直线方程为$y = k_2x + b_2$,将$(-2,7)$,$(3,1)$代入可得:
$\begin{cases}7=-2k_2 + b_2\\1 = 3k_2 + b_2\end{cases}$
两式相减消去$b_2$:$7 - 1=(-2k_2 + b_2)-(3k_2 + b_2)$,即$6=-5k_2$,解得$k_2=-\frac{6}{5}$。
把$k_2 = -\frac{6}{5}$代入$1 = 3k_2 + b_2$,得$1 = 3×(-\frac{6}{5})+b_2$,$b_2=\frac{23}{5}$。
所以直线方程为$y = -\frac{6}{5}x+\frac{23}{5}$。
3. 最后求两直线交点:
联立$\begin{cases}y=\frac{1}{6}x+\frac{9}{2}\\y = -\frac{6}{5}x+\frac{23}{5}\end{cases}$
即$\frac{1}{6}x+\frac{9}{2}=-\frac{6}{5}x+\frac{23}{5}$
通分:$\frac{5x}{30}+\frac{135}{30}=-\frac{36x}{30}+\frac{138}{30}$
移项:$\frac{5x + 36x}{30}=\frac{138 - 135}{30}$
$41x = 3$,$x=\frac{3}{41}$。
把$x=\frac{3}{41}$代入$y=\frac{1}{6}x+\frac{9}{2}$,$y=\frac{1}{6}×\frac{3}{41}+\frac{9}{2}=\frac{1}{82}+\frac{369}{82}=\frac{370}{82}=\frac{185}{41}$。
【答案】:$(\frac{3}{41},\frac{185}{41})$
查看更多完整答案,请扫码查看


