《2025年优秀生快乐假期每一天全新暑假作业本七年级合订本延边人民出版社》

2. 已知 $\sqrt{10} = 3.162$，$\sqrt{3} = 1.732$，$\sqrt{2} = 1.414$，求 $\frac{1}{3}\sqrt{10} - \sqrt{2} + 2\sqrt{3}$ 的值.（精确到 $0.01$）3.10

答案： 3.10

3. 设 $m$ 是 $\sqrt{13}$ 的整数部分，$n$ 是 $\sqrt{13}$ 的小数部分，求 $m - n$ 的值.

答案： $6-\sqrt {13}$

4. 细心观察右图，认真分析各式，然后解答下面的问题.

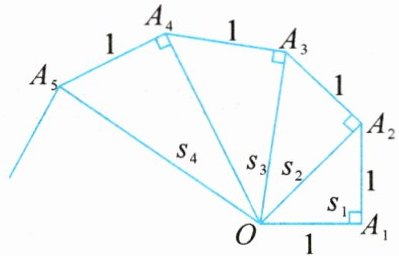
$(\sqrt{1})^{2} + 1 = 2$，$S_{1} = \frac{\sqrt{1}}{2}$；
$(\sqrt{2})^{2} + 1 = 3$，$S_{2} = \frac{\sqrt{2}}{2}$；
$(\sqrt{3})^{2} + 1 = 4$，$S_{3} = \frac{\sqrt{3}}{2}$；
……
（1）请用含 $n$（$n$ 为正整数）的等式表示上述变化规律.
$(\sqrt {n})^{2}+1=n+1,S_{n}=\frac {\sqrt {n}}{2}$
（2）推算出 $OA_{10}$ 的长度.
$\sqrt {10}$
（3）求出 $S_{1}^{2} + S_{2}^{2} + S_{3}^{2} + \cdots + S_{10}^{2}$ 的值.
$\frac {55}{4}$

答案：
(1) 规律如下：$(\sqrt {n})^{2}+1=n+1,S_{n}=\frac {\sqrt {n}}{2}$
(2) $OA_{10}=\sqrt {10}$
(3) $S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+... +S_{10}^{2}=(\frac {1}{2})^{2}+(\frac {\sqrt {2}}{2})^{2}+(\frac {\sqrt {3}}{2})^{2}+... +(\frac {\sqrt {10}}{2})^{2}=\frac {1}{4}(1+2+3+4+... +10)=\frac {1}{4}×55=\frac {55}{4}$

1.（山东青岛最新中考题）实数 $a$，$b$，$c$，$d$ 在数轴上对应点的位置如图所示，这四个实数中绝对值最小的是（C）

A. $a$
B. $b$
C. $c$
D. $d$

答案： C

2.（安徽最新中考题）我国古代数学家张衡将圆周率取值为 $\sqrt{10}$，祖冲之给出圆周率的一种分数形式的近似值为 $\frac{22}{7}$. 比较大小：$\sqrt{10}$＞$\frac{22}{7}$（填“$＞$”或“$＜$”）.

答案： $＞$